3-08-1：コンデンサーの5大公式 ＃その1

５大公式の最初の３つ「3大公式」をまず押さえるのが、コンデンサーを理解する早道です！　→　＜#その2＞は3-08-2へ　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

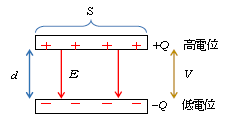
　２つの導体の一方に電荷\(Q\)(>0)、他方に\(-Q\)を帯電させた電荷をたくわえる装置をコンデンサーと呼ぼう。特に平行な２つの平板導体の組を「平行平板コンデンサー」、それぞれの導体を極板という（図１）。極板面積\(S\)が十分広く、極板間隔\(d\)が十分狭ければ、3-05-2でやった「平面電荷のつくる電場」の考え方を近似的に用いてよいことが実験的に確かめられている。高校物理で単にコンデンサーと言えば、ほとんどの場合「平行平板コンデンサーに平面電荷の考え方を適用したもの」を指す。空気中も真空中もコンデンサーのふるまいはほぼ同じだから、「真空中のコンデンサー」という言い回しもする。なお、「コンデンサーの電荷が\(Q\)である」とよく表現されるが、それは\(+Q\),\(-Q\)のペアが帯電しているという意味である。

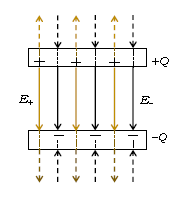
□ 第1公式
　図１で＋とーを互い違いに配置させたのは、あくまでも図を見やすくするため（そもそも＋やー(自由電子)の数は３個などではなく、ざっと10\(^{15}\)個程度ある）。+とーは逆符号電荷に働く引力によって、２つの極板の近い側(向かい合った側)に配列する。3-05-2でやった通り、＋のつくる黄色の電場は\(\displaystyle \)\(\displaystyle E_+=\frac{Q/\epsilon_0}{2S} \) 、ーのつくる黒の電場は\(\displaystyle E_ー=\frac{Q/\epsilon_0}{2S}\)、つまり大きさ\(E_+=E_ー\)である。極板間では\(E_+\),\(E_ー\)ともに下向きだから、
　合成電場は \(E=\)\(E_+ + E_ー=\)\(\displaystyle\frac{Q}{\epsilon_0 S} \)　これがポイント(1)である。
　平面１枚の電場は\(\displaystyle E_+=\frac{Q/\epsilon_0}{2S}\)のように分母に2が付いたが、極板が2枚のコンデンサーでは分母に2が付かない。また、点電荷のつくる電場は距離の2乗に反比例して小さくなるが、コンデンサーの極板間には平面電荷の場合と同様に、向きも大きさもいたるところ等しい一様電場ができる。
　(1)式は、運動方程式と同様の因果法則であることに注意しよう。運動方程式\(m\vec{a}=\vec{F} \)は「力\(\vec{F} \)が原因となって、結果的に加速度\(\vec{a} \)が生じる」と読む。(1)式は「電荷\(Q\)が原因となって、結果的に電場\(\vec{E} \)が生じる」と読む（電場が原因となって電荷が生じるのではない）。これは3-03-1の「電気分野全体のまとめ」 ―― 「電荷\(Q\)が電場\(\vec{E} \)をつくる」ですでに述べたこと。ゆえに(1)式こそコンデンサーの第１公式なのである。なお、コンデンサーでは\(\displaystyle E=\frac{1}{\epsilon_0 S} Q \)で、比例係数が\(\displaystyle \frac{1}{\epsilon_0 S}\) 。これは点電荷の\(\displaystyle E=\frac{k}{r^2} Q \)の比例係数\(\displaystyle \frac{k}{r^2} \)と異なるが、いずれにせよ結果\(E\)と原因\(Q\)は比例している（原因の\(Q\)が例えば３倍になれば、結果の\(E\)も３倍になる）ということが重要である。
　一方、極板間の上側では（図１）\(E_+\)が上向き、\(E_ー\)が下向きだから、打消し合って合成電場は０。極板間の下側でも\(E_+\)下向き、\(E_ー\)上向きで合成電場は０。つまり、コンデンサーの外部の電場は０である。言いかえると、（平面電荷の近似の範囲内で）コンデンサーはその外部に電気的な影響を及ぼせない。なお、コンデンサーの電荷の組合せが\(+Q,-Q\)だからこそ、極板内部の電場も０になっていることに注目しよう。これは3-06-1で述べた「導体内部の電場は0」の条件を満たす。絶対値の等しい＋とーの電荷が向かい合ってこそ、導体内部の電場が０になれる。
　以上をまとめたのがポイントの図である。

□ 第2公式
　3-04-1で電気力線に沿って電位の下り坂があると述べた。するとポイントの図から、＋の極板が電位が高く、ーの極板は電位が低く、その高低差（電位の下がり分）が電位差\(V \)である。
　3-04-1で電位差\(\Delta \phi \)=電場\(E\)×\(\Delta d \)　　　(＊)
という式を示し、注意点として、\(\vec{E} \)が一定でないときは\(\Delta d \)は正確には無限小に取ると述べた。コンデンサーでは電場は一様だから、\(\Delta d \)の代わりに有限の極板間隔\(d \)（ポイントの図）と書いてよく、(＊)の式を
　電位差 \(V=Ed \) と書く。これがポイント(2)である。

□ 第3公式
　(2)の\(V\)の式に(1)の\(E\)の式を代入すると、
　　\(\displaystyle V=\frac{Q}{\epsilon_0 S} d=\frac{d}{\epsilon_0 S} Q \) 　　　(☆)
となって、\(V\)が\(Q\)に比例する、言いかえると\(Q\)が\(V\)に比例することが分かる。この比例関係を \(Q=CV\)　と書き、\(C\)を容量（詳しくは電気容量または静電容量）という。つまり、容量の定義式は \(\displaystyle C=\frac{Q}{V}\) であるから、容量とは「単位電位差あたりたくわえられる電荷」という意味になる。同じ電位差で比較すると、たくわえる電荷が多い方が容量が大きい。つまり、容量とは「電荷のたくわえやすさ」とも言える。容量の単位は[C/V=F](ファラッド)。[mF][\(\mu\)F][pF](=10\(^{-12}\)F、ピコファラッドと読む）などがよく用いられる。
　(☆)より \(\displaystyle C=\frac{Q}{V}=\frac{\epsilon_0 S}{d}\)
　容量\(C\)は、\(S\)が分子にあることから分かる通り、極板面積\(S\)が広いほど大きい。面積\(S\)が広い方が、電荷をたくわえるスペースが広いのだから電荷がよりたくわえられ、容量(電荷のたくわえやすさ)\(C\)も大きい、というのは直観的に受け入れやすいだろう。
　(☆)の式変形で\(\displaystyle V=\frac{Q}{\epsilon_0 S} d\) の\(Q\)を分子から引きずり下ろすと\(\displaystyle V=\frac{d}{\epsilon_0 S} Q \) となって、\(V\)が\(Q\)に比例することが一目で分かる。このとき、\(Q\)の手前の係数\(\displaystyle \frac{d}{\epsilon_0 S} \) が\(\displaystyle \frac{1}{C}\)だ。というのも、\(Q=CV\)より\(V= \frac{1}{C}Q\)であるから。(☆)の式変形に慣れておくと、コンデンサーの上達も早い。