3-06-1: 静電誘導

静電誘導をしっかり押さえておくことが、コンデンサーの理解には重要です！

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　電気をよく通す物質を導体といい、金属や電解質水溶液などがその例。ここでは金属を例にとって導体の性質を説明していく。
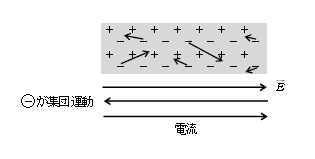
　まず、金属は正イオンと自由電子からなる（図１）。
　　正イオン(+)は規則正しく配列し、各々のつり合いの位置の周りに振動はするが、遠くへと移動していくことはない。
　　自由電子(ー)はふだんは平均速度が、その向きまで含めると０である。これを「電流０」の状態という（図１の灰色）。一方、電場をかけると、負電荷の電子は電場と逆向きに電気力を受けるため、ざっと\(\displaystyle \)10\(^{18}\)個程度の自由電子が電場と逆向きに集団運動し、平均速度が０でなくなる。この状態を「電流が流れている」という。歴史上の経緯で、電子(負電荷)の流れる向きと逆向きが電流の向きということになっている。
　　通常は正イオンと電子との電気量の絶対値どうしが等しい、すなわち電気的に中性の状態を扱う。

　この単元では「電荷が分布する」「電荷分布」という言葉を多用するが、それは、電荷が1個とは限らず複数ある場合を想定しての用語である。
　さて、導体を電場中に置いたとき（帯電体に近づけたとき）、電気力線の上り側に負電荷、下り側に正電荷が分布する（図２）。この現象を静電誘導という。図２(a)に示したのは、金属球が、その左横にある十分広い平面状の電荷分布（図には示していない）のつくる電気力線(黒)の中に置かれた様子。金属球の外の電荷分布による電場だから外場という。自由電子は外場と逆向きに力を受けて力線の上り側に移動し、負電荷(ー)が金属の左側表面に分布する。右側表面はー不足となって正電荷(＋)が分布する。新たに生じたー、＋のつくる電場（青）は金属球内では左向きで、右向きにかけた外場を弱める方向になっている。

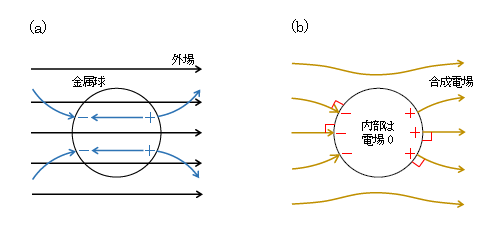
　この自由電子の移動により熱が発生する（一例として、電気ストーブは金属に電流を流して発生する熱を利用するもの）。つまり熱エネルギーの形でエネルギーを失っていき、やがては自由電子の移動は止まる。このとき金属の内部に合成電場は残っていない。なぜなら、電場が残っている間は、自由電子が電場から力を受けてまだ移動中であることを意味するから。外場と新たに生じたー、＋による電場との合成電場は、帯電完了後（すなわち自由電子の移動が止まった後）図２(b)のようになる。
　3-03-1でやった通り電気力線に沿って電位は下がるが、導体内部の電場は０だから電位が下がりようもない。つまり導体全体は等電位である（電位が上がったり下がったりしない）。数式で言い換えると、3-04-1の電位差\(\Delta \phi \)=電場\(E\)×電場方向に測った距離\(\Delta d \) の式で、\(E=0\)だから\(\Delta \phi =0\)、つまり電位差がないということである。全体が等電位だから、とくに導体表面は等電位面で、力線は等電位面と垂直だから電気力線と導体表面は互いに垂直である。
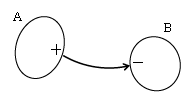
　2つの別々の導体A、Bがあったとして（図3）、その間に電気力線の生じることがある。力線に沿って電位は下がるのだから、AよりもBの方が電位が低い。つまり、AとBの電位は等しくない。正確には「ひとつながりの導体は等電位」（A全体は等電位、B全体も等電位）と覚えるべきだ。

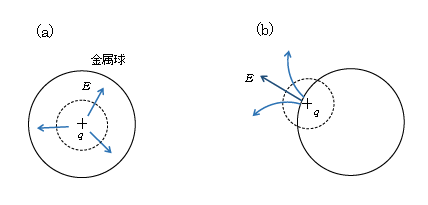
　さて、電荷分布が生じたとすると、図4(a)のように導体の奥深くに生ずることはない。なぜなら、かりに\(q\)(>0)の電荷分布が生じたとして、それを(a)のように導体内部の点線の閉曲面で取り囲む。3-05-1のガウスの法則によれば、閉曲面を\(\displaystyle 4\pi k q \) 本電気力線が貫くことになるが、これでは導体内部の電場が０でなくなるので矛盾である。よって、図4(b)のように電荷分布は導体表面にしか生じない。(b)のように電荷分布\(q\)を点線の閉曲面で囲んだとしても、\(\displaystyle 4\pi k q \) 本の力線全てが導体外部へ逃げていく場合が想定できて、何も矛盾は生じない。なお、(b)のような力線は、もちろん単独の電荷がつくり出すものではなく、\(q\)と書かれているのは多数個からなるまさに「電荷分布」の意味である。