1-44-1: ばねの両端につないだ2物体 ー 重心運動

この単元からは入試の頻出問題「ばねの両端につないだ2物体」というテーマがしばらく続きます。！　→　＜続き＞は1-45-1,1-45-2,1-45-3,1-45-4へ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　「ばねの両端につないだ2物体」というタイトルは少々長いので、今後説明文中では「ばね相互作用」という語句で表現したい。これから5つの単元にわたっていろいろな切り口で、ばね相互作用の問題を扱っていくことにしよう。その1つ目が、タイトルの「重心運動」である。
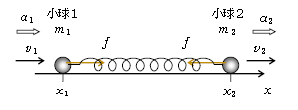
　さっそく運動方程式から。自然長\(l\)、ばね定数\(k\)の軽いばねの両端に、図１のように質量がそれぞれ\(m_1,m_2\)の小球1,2(以後単に球と呼ぶ)をつなぎ、なめらかなで水平な床の上に置く。床に沿って右向きを正とする\(x\)軸を取る。任意の時刻\(t\)での球1,2それぞれの\(x\)座標を\(x_1,x_2\)、速度を\(v_1,v_2\)、加速度を\(a_1,a_2\)とする。ばね相互作用においては、それぞれに働く力の\(x\)成分は弾性力のみを想定していて、その大きさをばねが伸びていると仮定して\(f\)と図示してある（ばねが縮んでいる場合の説明はまもなくするとしよう）。ばねは自然長に戻りたがる性質がある(1-14-1)から、伸びたばねは両端を引張る向きに力を及ばす。なお、「（軽い）ばねは両端に等しい大きさの力を及ぼす」。これは本来証明できることとはいえ、とりあえずはばねの性質として覚えておこう。時刻\(t\)でのばねの長さは\(x_2-x_1\)で、のびの長さとは自然長からどれだけ伸びたかの量だから、(のび)\(=x_2-x_1-l\)　
　弾性力の大きさ\(f=k\)×(のび)(1-14-1)\(=k(x_2-x_1-l)\)　　

　運動方程式は
　球1: \(m_1a_1=+f=+k(x_2-x_1-l)\)　　　(1)
　球2: \(m_2a_2=-f=-k(x_2-x_1-l)\)　　　(2)
　ばねが伸びていると仮定したが、縮んでいると仮定したなら図２のようになる。自然長に戻りたがって縮んだばねは両端を等大の力\(f’\)で押す。縮んでいるがゆえに、自然長\(l\)よりも、時刻\(t\)でのばねの長さ\(x_2-x_1\)の方が短い。ちぢみの長さとは自然長からどれだけ縮んだかの絶対値だから、(ちぢみ)\(=l-(x_2-x_1)\)
　弾性力の大きさ\(f’=k\)×(ちぢみ)\(=k(l-(x_2-x_1))\)
　図１より、伸びているときは\(x_2-x_1>l\)だから、\(f=k\)×(のび)\(=k(x_2-x_1-l)\)だった。
　ところが、縮んでいるときは\(l>x_2-x_1\)だから、\(f’=k\)×(ちぢみ)\(=k(l-(x_2-x_1))\)。すなわち、数式上では\(f’=-f\)になっていることに注意しよう。図２の運動方程式は
　球1: \(m_1a_1=-f’=+f=+k(x_2-x_1-l)\)　　(1′)　　　
　球2: \(m_2a_2=+f’=-f=-k(x_2-x_1-l)\)　　(2′)　
(1′),(2′)は(1),(2)と全く同値である。このように、伸びていると仮定しても縮んでいると仮定しても、運動方程式は変わらない。つまり、のび・ちぢみ両方の場合を調べる必要はなく、どちらか一方の図を書いて運動方程式を立てればそれで済む（このことは、小球が１つの場合については1-22-1で説明してある）。

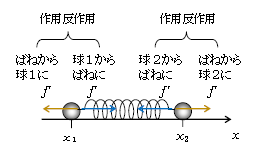
　ところでばね相互作用は、2球の関わる2体問題というよりも、正確には2球にばねを加えた3体問題である（ただし、軽いばねを考えているから、ばねの質量は入れない）。弾性力\(f’\)は、図３を見て分かる通り3体のうちの2体どうしの（ばねと球1あるいはばねと球2どうしの）作用反作用だから、内力である(1-31-1)。ばね相互作用では外力(3体以外から加わる力)がない。一方、1-43-1で述べたように「重心は外力\(F_外\)のみによって加速される(内力は無関係)」。ということは、重心の加速度は０であることが期待される。そこで、球1,2の重心Gの運動方程式を求めよう。そのために、(1′)+(2′)を\(m_1+m_2\)で割る。
　\(\displaystyle \frac{m_1a_1+m_2a_2}{m_1+m_2}=\frac{-f’+f’}{m_1+m_2} \)
　左辺は1-43-1で扱った重心加速度\(a_G\)、右辺は0。つまり、\(a_G=0\)、予想通り重心Gは加速しないことが分かった。言い換えると、ばね相互作用では重心Gは等速直線運動を続ける。初め静止していれば静止し続ける。

　ここで、重心運動のイメージの話を一つ。水素分子\(\text{H}_2\)を例に取ろう。もちろん\(\text{H}_2\)は目に見えない極めて小さな対象だが、あたかも目に見えるかのようにイメージすることにし、重力は無視しよう。1-43-1の通り重心は、２つの\(\text{H}\)原子を質点のように見なして、その位置を質量の逆比に内分する点。\(\text{H}\)原子どうしの質量比は1:1だからその逆比も1:1、すわなち重心は\(\text{H}_2\)分子の中点に位置する。仮に\(\text{H}_2\)を野球のバットで叩いたなら、\(\text{H}_2\)に外力(バットからの力)が働いて重心は加速する。一方\(\text{H}_2\)を放っておけば、外力が働かないから重心は加速しない、等速直線運動を続ける(初め静止していれば静止し続ける)。ばね相互作用の重心Gは、球1,2の位置を質量の逆比\(m_2:m_1\)に内分する点。その点Gが（ばねが伸びたり縮んだりをするにせよ）、一定のペース(等速)で進んでいく。
　さて、ばね相互作用の重心Gが等速であるとは、1-43-1で扱った
　重心速度\(\displaystyle v_G=\frac{m_1v_1+m_2v_2}{m_1+m_2}=\)一定
であることを意味する。分母の\(m_1+m_2\)は一定だから、分子の\(m_1v_1+m_2v_2\)も一定。すなわち、ばね相互作用では運動量保存が成り立っている。このように、重心が等速であることと、運動量が保存していることとは、同値である。運動量保存則の成立条件は、1-31-1の通り外力がないことだった。ゆえにまとめると、「ばね相互作用では外力がないから、運動量が保存するとともに、重心が等速である。」