3-05-2: ガウスの法則の応用例:平面電荷
ガウスの法則の重要な応用例をしっかりマスターしましょう!コンデンサーの理解に欠かせません。
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 平面電荷のつくる電場:平面に垂直な一様電場で、
強さ\(\displaystyle E=\frac{Q/\epsilon_0}{2S} \)
\(S\): 平面内にとった面積 \(Q\): 面積\(S\)内の電荷
\(\epsilon_0\): 真空の誘電率
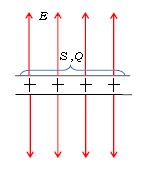
図1(a)のように、無限平面上に点電荷が一様に分布している(ある所は電荷が密集していたり、また別の所はまばらだったりすることがない)場合を「平面電荷」と呼ぶことにする。それを手前から見て平面を水平にした断面図が図1(b)。各々の+は点電荷\(q\)(>0)であるとし、平面の厚みを無視する。+どうしの間隔は等しい。まずはクーロンの法則の考え方で、平面電荷のつくる電場\(\vec{E} \)がどのようになるのかを考察しよう。
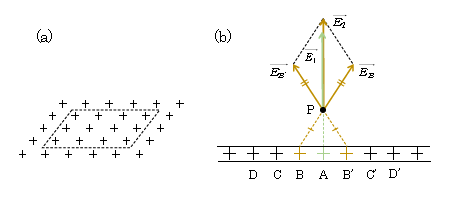
図の点Pで、点Pの真下の+(A)がつくる電場\(\vec{E_1} \)(緑)は明らかに平面に垂直で上向き。+(A)の両隣の+(B,B’)がつくる合成電場\(\vec{E_2}=\vec{E_B}+\vec{E_{B’}} \)(黄)も平面に垂直で上向き、なぜなら、距離\(r=\)PB=PB’だから\(\displaystyle E_B=E_{B’}=k\frac{q}{r^2} \)(3-02-1)で、平行四辺形の合成則が直線APに関して左右対称な菱形の合成となるからである。同様にして、さらに両隣の+(C,C’)のつくる合成電場\(\vec{E_3} \)も平面に垂直で上向き、そのまた両隣の+(D,D’)のつくる\(\vec{E_4} \)も平面に垂直で上向き、・・・。以上の考察を、平面を真上から見たときの様々な方向の断面で繰り返せば(図2(a))、点Pの(全合成)電場\(\vec{E_P} \)は平面に垂直で上向きと分かる(図2(b))。
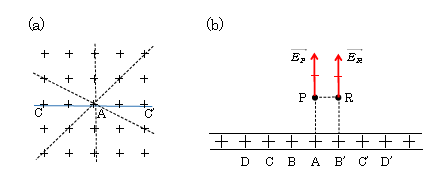
これ以外にも点線の断面など、切り取り方は様々ある。
今度は平面からの距離が点Pと等しく、かつ点B’の真上の点Rを考える(図2(b))。全く同様に、電場\(\vec{E_R} \)は平面に垂直で上向きと分かる。しかも平面は無限に広いことから、点Pについて両隣(B,B’)、両隣(C,C’)、両隣(D,D’)、・・・と組んだペアの数は、点Rについて両隣(A,C’)、両隣(B,D’)、・・・と組むペアの数と等しい。ということは電場の強さ\(E_P=E_R \)である。結局、以下のような結論になる(図3に電気力線の概要を示した)―――
<平面電荷のつくる電場> 向き:いたるところ平面に垂直
強さ:平面から同じ距離なら同じ強さ (☆)
ここまではクーロンの法則に基づいて考えてきたが、いざ電場の強さを計算するとなると、無限個の電荷\(q\)のつくる電場を合成しなければならず、事実上高校の範囲外である。そこで、ここからはガウスの法則の考え方に切り替える。
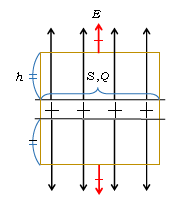
図3では、平面電荷を底面積\(S\)、高さ\(2h\)の直方体ではさみ込んである。直方体内部の電荷の合計を\(Q\)としよう。3-05-1と同様に、
閉曲面(直方体)を貫く力線の総数 \(=\) 1m\(^2\)あたり\(E\)本 × 力線が貫く表面積\(2S\) (1)
\(\displaystyle\)力線が貫く表面積が\(2S\)である理由は ―― 直方体は全部で6枚の面を持ち、このうち4枚の面(右、左、手前、奥)は力線がその面に接してはいるものの、その面を貫いて(串刺しにして)はいない。上、下2枚の面だけを力線は貫いて(串刺しにして)いるからである。3-05-1より、(1)の左辺が\(\displaystyle \frac{Q}{\epsilon_0}\) と書けるから、
平面電荷のつくる電場\(\displaystyle E=\frac{Q/\epsilon_0}{2S} \) (2)
ガウスの法則を用いると、あっという間に電場の強さが計算できたことに注目してほしい。ただし、これは(☆)に述べた特殊な事情があったからで、そうでない場合はあっという間に計算などできない。(☆)を「平面対称性」のある電場という。(ガウスの法則が役に立つのは、高校物理では後は球対称、球殻対称、円柱対称な場合ぐらいである。)
式(2)の覚え方としては、1m\(^2\)あたりの力線の本数が\(E\)本であることから、
「\(E\)は総数\(\displaystyle \frac{Q}{\epsilon_0}\)本を上下の面積\(2S\)で割ったもの」
と理解しつつ覚えるのがよい。なお、(2)中の\(\displaystyle \frac{Q}{S} \)[C/m\(^2\)]を面電荷密度\(\sigma\)と呼んで、(2)の
\(\displaystyle E=\frac{Q/S}{2\epsilon_0}=\frac{\sigma}{2\epsilon_0} \)と表すこともある。
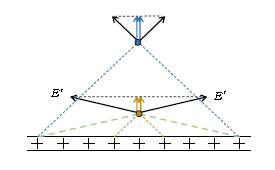
ところで、図3で直方体の高さ\(2h\)を低く取ろうが高く取ろうが、直方体内部の電荷が\(Q\)であることには変わりがない。ということは、(1)の左辺が\(Q/\epsilon_0\) であることに変わりはないから、(2)の電場\(E\)の公式は\(h\)の大小によらないということになる。よって、平面電荷のつくる電場は、平面の上側・下側についてそれぞれ一様電場(向きも大きさもいたるところ等しい電場)である。各々の電荷\(q\)のつくる電場は距離の2乗に反比例して弱くなっていく(3-02-1)のにもかかわらず、電荷が無数集まると距離\(h\)によらない一様な電場ができるというのだ。
その直観的な説明を与えるのが図4。平面に近づくと、(1個の電荷のつくる)電場\(E’\)の大きさ自体は大きくなるが、電場\(E’\)が傾きすぎるので\(E’\)の平面に垂直な成分が大きくなるかどうかは微妙である(青と黄の上向き矢印を比較せよ)。また平面に近づくと、電場の平面に対する傾きを大きくするような電荷の数も少なくなる(青の斜めの点線の内側に含まれる+の数が例えば9個であるのに対して、青と同じ傾きに取った黄の斜めの点線の内側に含まれる+の数は3個)。ゆえに、電場の平面に垂直な成分が大きくなるかどうかはやはり微妙なのである。(参考までに、電場は距離の2乗に反比例であることから、緑の点線に沿う向きの電場の強さ\(E’\)に対して、黄色の点線に沿う向きの電場の強さは(図示していないが)約\(10E’\)である。また、紙面に垂直な方向も考慮しなければならないことをお忘れなく。)