1-32-1: 2体問題 <例題> ー 力学攻略の基本 第4弾 <動画あり>
2体問題はしばしば運動量保存則がカギとなります!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 2体問題は、2体全体に広く目を配って「外力はどれか?」と問おう
2体問題とは、2物体が互いに絡み合いながら運動するタイプの問題で、入試の頻出テーマである。
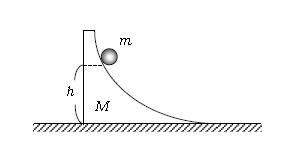
例えば図1。なめらかな曲面をもつ質量\(M\)の台をなめらかで水平な床の上に置き、その曲面上の床から高さ\(h\)の所に質量\(m\)の小球を置く。初め台と小球をともに手で支えて静止させておき、両方から同時に静かに手をはなすと、小球は曲面を下っていく。小球が床に達したときの小球及び台の速さを求めてみよう。重力加速度を\(g\)とする。
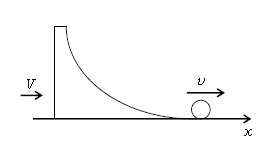
床に達したときの小球、台の速度を図2のように右向きを正としてそれぞれ\(v,V\)と図示する、おく。ただし、速度が負の値で求まったなら負の向きへ動くという意味であって、決して正の向きへ運動中という意味の図ではない(この図の書き方は1-31-2と同様である)。
ここで、
例題
\(v,V\)を求めよ。
解答・解説
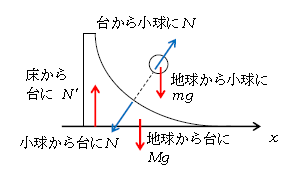
さて、力学という分野は何といっても1-08-1: 力学攻略の基本 が根幹である。つまり、まずは軸と力を書き込む(図3)。
次に1-08-1にならって\(ma=F\)と行きたいところだが、曲面を下るにつれ次々と小球の加速度の向きが変化していく(等加速度ではない)し、そもそも曲面の形状も与えられているわけではない。\(ma=F\)では明らかに行き詰まってしまう。
そこで、2体問題を解くときには、2体全体に広く目を配って「外力はどれか?」と問う意識付けが極めて重要になる。
1-31-1でやった通り、外力とは注目している2物体(台と小球)以外から働く力だから、図3の赤い矢印(地球から小球に、床から小球に)は外力である。
一方、内力とは注目している2物体どうしで及ぼし合う作用反作用のペアだから、青い矢印。
すると、とっさに外力が鉛直方向に揃っている、水平方向には外力がない、と気付くであろう。
あとは、水平方向に外力がないから水平方向の運動量保存が成り立つ(1-31-1)と行ければ、シメタもの。
これと力学的エネルギー保存を連立すれば、式が2つ、未知数が\(v,V\)の2つで解ける。
図1をまえ状態、図2をあと状態として、
あと まえ
水平方向の運動量保存 \(mv+MV\) \(=\) \(0\) (1)
力学的エネルギー保存 \(\displaystyle \frac{m}{2}v^2+\frac{M}{2}V^2\) \(=\) \(mgh \, \) (2)
[ 床を高さ0に取って、まえ状態の位置エネルギーは\(mg0+Mg0\)という意味 ]
(1)より \(\displaystyle V=-\frac{m}{M}v \) (3)
(2)に代入 \(\displaystyle \frac{m}{2}v^2+\frac{M}{2}\frac{m^2}{M^2}v^2 =mgh \)
∴ \(\displaystyle \frac{m}{2}v^2 \left( 1+\frac{m}{M} \right)=mgh \) ∴ \(\displaystyle \frac{m}{2}v^2\frac{M+m}{M}=mgh \)
∴ \(v=\) 答 \(\displaystyle \sqrt{ \frac{M}{M+m}2gh } \)
(3)より 答 \(\displaystyle V=-\frac{m}{M} \sqrt{ \frac{M}{M+m}2gh } \)
\(V<0\)と求まる理由は、図3の小球から台に働く\(N\)が斜め左向きで、台が(\(x\)軸を右向き正として)左向きに押されるからである。
なお、michisanpo.youtubeにある関連動画も是非参考にしてみて下さい。よければチャンネル登録お願いします。
https://www.youtube.com/watch?v=svRixzPfXV8


