3-08-2: コンデンサーの5大公式 ＃その2

3-08-1に引き続き、第４，５公式をポイント(4),(5)にまとめました。　　　　　　　　　　　　　　　　　

□ ポイント(4)について
　極板間引力\(F\)とは、正極板(\(+Q\)側)と負極板(\(-Q\)側)の逆符号の電荷どうしに働くクーロン引力（図１(a)）のことで、作用反作用のペアになっている。下向きの\(F\)は\(-Q\)が\(+Q\)を引張る力、上向きの\(F\)は\(+Q\)が\(-Q\)を引張る力。3-02-1で述べた式\(\vec{F}=q\vec{E} \)は、１個の電荷\(q\)が電場\(\vec{E} \)中で受ける電気力\(\vec{F} \)を表す。ところがコンデンサーでは電荷\(+Q\)は無数(ざっと10\(^{15}\)個程度)の正イオンから成り、１個の場合と少し事情が異なる。結論を先に言えば、\(\displaystyle F=QE \)とはならず、
　ポイント(4)のように　\(\displaystyle F=Q\frac{1}{2} E \)　と\(\displaystyle \frac{1}{2}\)が付く。

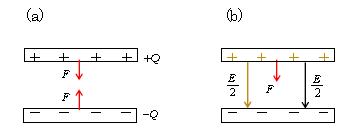
　その理由はこうだ。3-08-1でやった通り、コンデンサーの電場\(E\)は（図１(b)）正極板のつくる\(\frac{1}{2} E\)(黄色)と負極板の\(\frac{1}{2} E\)(黒)との和である。ところが正極板は自身のつくった\(\frac{1}{2} E\)(黄色)から力を受けたりはしない。これは、点電荷\(q\)が自身のつくった電場\(E\)から力を受けてひとりでに動き出したりしないのと全く同様である。（これについては、運動方程式の単元に記した「我々の宇宙は他から(周囲から)力が働いて初めて加速度が生じるようにできている。…物体が物体自身に力を加えることによって勝手に動き出す(速度を増やす)、などということは決して起こらない」を思い出そう。）正極板は、ひとえに相手の負極板のつくる\(\frac{1}{2} E\)(黒)のみから力を受ける。よって\( F=Q\frac{1}{2} E \)となるのだ。
　なお、3-08-1の電場の式\(\displaystyle E=\frac{q}{\epsilon_0 S} \)を代入すると、\(\displaystyle F=\frac{Q^2}{2\epsilon_0 S} \)となって、極板間引力(電気力)\(F\)はやはり電荷の積\(Q^2\)に比例することが分かる。

□ ポイント(5)について
　コンデンサーの持つエネルギーを静電エネルギー\(U\)という。「コンデンサーがエネルギーを持つ」とはどういうことだろう？ここで、1-17-1の重力による位置エネルギーの定義を思い出すと、「基準点から高さ\(h\)の所にある物体に対して、基準点まで重力がすることのできる仕事」が位置エネルギーとある。そう、エネルギーとは「仕事をする能力」のことだった。コンデンサーの場合、仕事する能力とは「電荷\(Q\)から電荷が０になるまでコンデンサーの電場\(E\)がすることのできる仕事」\(W\)を指し、これを静電エネルギー\(U\)(\(=W\))と呼んでいる。
　図２(a)はコンデンサーが\(Q\)たくわえている状態、(c)はすっかり電荷が０になった状態、(b)はその途中の電荷が(任意の)\(q\)(>0)の状態。上の極板の\(q\)から微小な電荷\(\Delta q\)を剥ぎ取ると、一時的に上の極板の電荷が\(q-\Delta q\)に減ることに注意。すると、3-08-1の電場の式\(\displaystyle E=\frac{q}{\epsilon_0 S} \)も微小量\(\Delta E\)減るはずで\(E-\Delta E\)とおける。\(\Delta q\)に働く微小な電気力は
　\(\Delta F=\Delta q(E-\Delta E)=E\Delta q-\Delta q\Delta E \) 　　　　(＊)
　\(\displaystyle \)この\(\Delta q\Delta E \)は\(\Delta\)が２回かけ算されたもので「２次の微小量」という言い方をする。ただでさえ\(\Delta\)は「ものすごく小さい量」（例えば0.000…1よりさらに小さい）なのだから、２次の微小量は無視してよい。これは物理の全分野で使える常套手段だ。すると、(＊)の\(\Delta F=E\Delta q\) となって、微小な減少量\(\Delta E\)のことは心配せず安心して\(\displaystyle E=\frac{q}{\epsilon_0 S} \)を使える。と言うよりも、安心してこの\(E\)の式を使うために、剥ぎ取る電荷は微小量\(\Delta q\)としたのである。結局(＊)より、\(\displaystyle \Delta F=\frac{q}{\epsilon_0 S} \Delta q \) 。

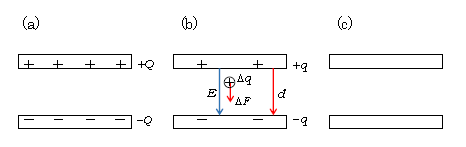
　\(\Delta q\)が上極板から下極板に達する移動距離\(d\)（図２(b)）において、電場\(E\)のする微小な仕事は
　　\(\displaystyle \Delta W=\Delta F \cdot d =\frac{q}{\epsilon_0 S} \Delta q \cdot d=\frac{d}{\epsilon_0 S} q\Delta q=\frac{1}{C} q\Delta q \)　　(☆)
（3-08-1の容量\(C\)の式を用いた）。\(\Delta q\)が下極板に達した時点で、上下極板の電荷はそれぞれ\(q-\Delta q\)、\(-(q-\Delta q)\)になっている。後はこの\(\Delta q\)を距離\(d\)運ぶ操作を何回も何回も繰り返し、最終的に図２(c)まで持って行ったときの微小仕事の総和\(W=\Sigma \Delta W\)を計算すれば、「電荷\(Q\)にコンデンサーの電場\(E\)がすることのできる仕事\(W\)」すなわち静電エネルギー\(U＝W\)が求まる。
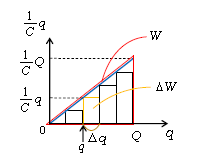
　さて、総和\(W=\Sigma \Delta W\)の計算であるが、グラフ的手法を用いてみよう。図３で横軸を\(q\)、縦軸を\(\frac{1}{C} q \)に取ると、傾き\(\frac{1}{C} \)の直線のグラフ（青）が書ける。これを横幅\(\Delta q\)ごとの階段グラフに区切ろう。最後には\(\Delta q → 0 \)の極限を取るから、階段グラフは直線のグラフと一致する。階段グラフの長方形１個分(黄色)の面積は\(\displaystyle \frac{1}{C} q × \Delta q \)で(☆)の\(\Delta W \)と等しい。すると総和\(W=\Sigma \Delta W\)は階段グラフの面積の極限すなわち赤い三角形の面積となる。
　よって\(\displaystyle W=Q×\frac{1}{C}Q÷2 \)　つまり \(U=\)\(W=\)\(\displaystyle \frac{Q^2}{2C} \)　これがポイント(5)である。
　あとは3-08-1の\(Q＝CV\)を代入すると　\(\displaystyle U=\frac{1}{2}CV^2\)　もう１回代入すると　\(\displaystyle U=\frac{1}{2}QV\)　も言える。
　なお、このグラフ的手法は有名でよく出題もされるから、一回理解したらそのやり方を覚えてしまおう。