1-05-1: 運動方程式
運動方程式は力学という大樹の幹。きっちり理解しておきましょう! → 1-06-1: 力学攻略の基本、1-07-1: 運動方程式を立ててみよう へ続く
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
運動方程式は数学のベクトル記号\(\vec{a},\vec{F}\)を用いて書かれるが、以下では簡単のため普通に\(a,F\)のように表記する。なお、本参考書では単元1-15-1までベクトル記号をほとんど用いないことにする。
ポイント
・ 運動方程式(ニュートンの運動の第2法則) \(ma=F\)
ベクトル記号を用いると \(m\vec{a}=\vec{F}\)
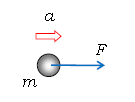
\(m\): 物体の質量 [\(\text{kg}\)]
\(a\): 物体の加速度 [m/s\(^2\)]
\(F\): 物体に加わる合力 [N]
・ つり合いとは合力0のこと
・ 慣性の法則(ニュートンの運動の第1法則)「物体に加わる合力が0ならば、物体は等速直線運動を続ける。初め静止していれば静止し続ける」
なお、\(m\)は符号・向きを持たない。\(a, F\)は符号・向きを持つ。
運動方程式\(ma=F\)を理解するときには、むしろ右辺から左辺に読むのがいい。「力\(F\)(右辺)が加わると、加速度\(a\)(左辺)が生じる」と読む。右辺の力\(F\)とは、物体の速度を変化させる原因。確かに、物体に指で力を加えれば速度は変化する。左辺の加速度\(a\)とは、1sあたりの速度変化で、力という速度変化の原因によって生じるもの。ゆえに運動方程式\(ma=F\)は、「力\(F\)という速度変化の原因によって、結果的に加速度\(a\)が生じる」「原因から結果が生まれる」と読む。運動方程式は「因果法則」であるという言い方もする。
力の単位は[N](ニュートン)。質量1\(\text{kg}\)の物体に、結果として1m/s\(^2\)の加速度を生じさせるような原因の大きさを、1Nと決める。つまり\(ma=F\)より 1\(\text{kg} \)×1m/s\(^2\)=1N 、 [N=\(\text{kg} \cdot \)m/s\(^2\)] だ。
さて、運動方程式\(ma=F\)はなぜ成り立つのか、と聞かないでほしい。むしろ、我々の宇宙は\(ma=F\)が成り立つようにできているという仮説を置いて、それが実験事実を見事に説明するから、\(ma=F\)は成り立つと認めているのである。\(ma=F\)の成り立たないまた別の宇宙があるのかもしれないが、そんな宇宙があるかどうかの答は現在の物理学にはない。ともかく我々の宇宙においては、\(ma=F\)を力学の出発点の式として認めよう。この出発点の式という意味において運動方程式を、力学分野における「宇宙の根本原理」と呼ぶことにしたい。
この意味で、我々の宇宙は他から(周囲から)力が働いて初めて加速度が生じるようにできている。物体の速度を変化させる原因(力)は必ず他から(例えば手から)加わる。物体が物体自身に力を加えることによって勝手に動き出す(速度を増やす)、などということは決して起こらない。
運動方程式\(ma=F\)を用いると、結果としての加速度\(a\)が求まる。その例として ―― 下図で\(F_1\) , \(F_2\)は力の大きさを意味し、符号を持たないとして図示している。が、式\(ma=F\)中の\(F\)は合力(力の合計)を意味し、符号を持つ。具体的には、\(x\)軸の正の向きを例えば右向きに取ると、正の向きの力\(F_1\)はプラス\(F_1\)とし、負の向きの力\(F_2\)はマイナス\(F_2\)とする。すると、合力(力の合計)\(F=F_1-F_2\)で
\(ma=F=F_1-F_2 \)
∴ \(\displaystyle a=\frac{F_1-F_2}{m} =\frac{3-6\: \text{N}}{2\: \text{kg}} =\frac{-3\: \text{kg \(\cdot\)m/s\(^2\)} }{2\: \text{kg}}=-1.5 \text{m/s}^2 \)
(なお ∴ という記号は「ゆえに」と読む。念のため。)
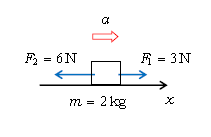
ここで\(a\)は符号を持つ量で、求まるまでプラスになるのかマイナスになるのか分からない未知量だから、とりあえず正の向きに\(a\)と図示する。いま\(a=-1.5 \text{m/s}^2\)のように負で求まったので、実は\(a\)は負の向きだったと後で解釈すればよい。
特に\(F_1=F_2\)のときは合力\(F=F_1-F_2=0\)。合力0のことをつり合いという。合力\(F=0\)なら、\(ma=F=0\)、ゆえに\(a=0\)、物体の速度は増えない、等速のまま。つまり、「物体に加わる合力が0(つり合い)ならば、物体は等速直線運動を続ける。初め静止していれば静止し続ける」。これを慣性の法則(ニュートンの運動の第1法則)という。[ 実は慣性の法則にはもっと深い意味合いもあるのだが、ここでは触れない。なお、この深い意味合いについて興味がある人は10-01-1を参照のこと。]
つり合いの式は、よく
0=\(F_1-F_2\)
のように書く。これはもちろん\(ma=m0=0=F_1-F_2\) のことである。


