3-04-1: 等電位線 ; 電場と電位差の関係
目に見えずにイメージしづらい電気現象を明快に解説していく招待状の第3弾、最後です。 → 3-02-1が第1弾、3-03-1が第2弾
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 電気力線と等電位線は直交する
・ 電位差(または電圧)\(\Delta \phi \)=電場\(E\)×電場方向に測った距離\(\Delta d \)
ここで\(\Delta \phi, \, E, \, \Delta d \)は全て絶対値(>0)の意味
\(\vec{E} \)が一定でないときは、\(\Delta d \)は正確には無限小に取る
・ 電場の強さ\(E\) \(=\) \(\displaystyle \frac{\Delta \phi}{\Delta d}\) 電位の下り坂の傾き
・ 等電位線の間隔が狭い所ほど電場は強い
3-03-1で「電気力線の向きに電位\(\phi \)は下がる」と述べた。ここで電位の等しい各点各点を結ぶと等電位線(立体的に表現すると等電位「面」)が書ける(図1)。青が例えば+1V一定のままの等電位線、黄は+2V、赤は+3Vの等電位線。地図で例えるなら等電位線は等高線に相当している(等高線は紙面に垂直な方向の高低を表す)。すると、電気力線は坂道のようにイメージして、「電気力線の向きに電位の下り坂がある」、電位の下り坂を駆け下りれば運動エネルギーが増える、となる。ここまで来ると、とかく目に見えずにイメージしづらかった電気現象が、電場という地図上の電位の高低(1Cあたりの位置エネルギーの高低)に置き換えられて、かなり扱いやすくなっている。
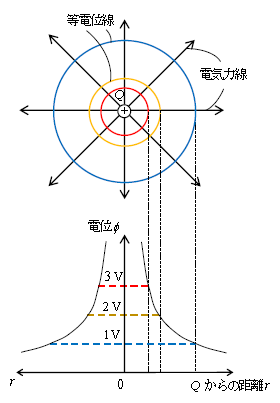
ここで電気力線と等電位線の重要な関係を4つ押さえていこう。
1⃣ 電気力線と等電位線は直交する(図2) ―― なぜなら、電気力線の向き(電場の向き、すなわち1Cあたりの力の向き)と垂直に動いたとすると、力の向きと移動の向きが垂直だから仕事が0。仕事が0だと、運動エネルギ―変化=仕事 より運動エネルギーが一定。すると力学的エネルギ―保存により位置エネルギーが一定。よって電位(1Cあたりの位置エネルギー)が一定で、電気力線の向きに垂直な方向は等電位線だと分かる。直観的には、等高線と垂直に動くと、坂道を真っ逆さまに降りていくイメージ(あらためて図1)。
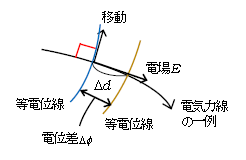
2⃣ \(|\Delta \phi| \)を通常単に\(\Delta \phi \)と書いて電位差あるいは電圧[V]と呼ぶ。電位差とはある地点の電位と別の地点の電位の「差」だから、地図で言えば高低差に相当する量。ところで重力による位置エネルギーの差(変化分)\(mgh\)とは、仕事=重力\(mg\)×重力の方向に測った距離(下降距離)\(h\) であることから分かる通り、
電位差(1Cあたりの位置エネルギーの差)\(\Delta \phi \)=1Cあたりの仕事
=1Cあたりの力×電場の方向に測った距離=電場\(E\)×\(\Delta d \) (図2)
3⃣ すると \(\displaystyle E=\frac{\Delta \phi}{\Delta d}\) (☆)
[N/C = V/m]
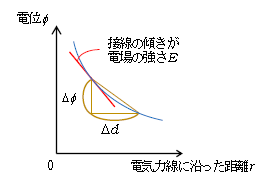
図3の青い曲線は、縦軸に電位\(\phi \)、横軸に電気力線に沿った距離\(r\)を取ったグラフの一例で、\(\displaystyle \frac{\Delta \phi}{\Delta d}\)は黄色の直角三角形のタテ÷ヨコ、つまり斜辺の傾きである。正確には\(\Delta d \)を限りなく小さく取って無限小にするから、斜辺の傾きは接線の傾きに一致し、電場の強さ\(\displaystyle E=\frac{\Delta \phi}{\Delta d}\) は \(\phi \)-\(r\)グラフの接線の傾き、すなわち電位の下り坂の傾きに等しいことが分かる。
(☆)式より、電場の単位はN/C と V/m の2通りの表し方がある。
\(\displaystyle \frac{\text{V}}{\text{m}} =\frac{\text{J}}{\text{C}} \cdot \frac{1}{\text{m}} =\frac{\text{N} \cdot \text{m}} {\text{C}} \cdot \frac{1}{\text{m}} =\frac{\text{N}}{\text{C}} \) だから、もちろん N/C と V/m は等しい。
電荷⊕のつくる等電位線、⊝のつくる等電位線、⊕⊕、⊝⊝、⊕⊝のつくる等電位線は、電気力線と相まって覚えてしまい手書きできるようにしておこう(⊕と⊝の電気量の絶対値は等しいとする)。そうすれば目に見えない電気現象の理解が格段に深まる。
⊕のつくる等電位線は図1の通り。⊝のつくる等電位線は図1と概形は等しいが、電位\(\phi \)の公式より\(\displaystyle \phi=k\frac{-Q}{r}\)<0となるから、「マイナス○○V」という値を持つ等電位線である。
⊕⊝の等電位線は図4左の太線(電気力線は細線)で、数値例を10V、\(-\)5Vのように示してある。電気力線の向きに電位が10,5,0,\(-\)5,\(-\)10Vと下がっていく様子が見て取れる。⊕⊕の等電位線は図4右で電位の値はプラス。⊝⊝の等電位線は⊕⊕の等電位線と同じ概形だが、電位の値はマイナスである。
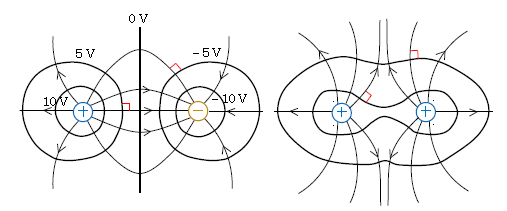
電気力線と等電位線は直交する(本文1⃣)
4⃣ 等電位線の間隔が狭い所ほど電場は強い。その理由は ―― 図4左に5V間隔で等電位線が引いてあるが、同じ電位差\(\Delta \phi \)=5Vに対しても、電場(電気力線)方向に測った距離\(\Delta d \)が大きい場所もあれば小さい場所もある。(☆)式より\(\Delta d \)が小さいほど電場の強さ\(E\)は大きいから、等電位線の間隔が狭い所ほど電場は強いと言える。これは地図のイメージでいえば、等高線の間隔が狭い所ほど坂道の傾きが急であることに相当している。


