2-14-1: ドップラー効果の別証明 ＜動画あり＞

michisanpo – YouTubeで関連動画をまず見てから、この単元の学習に入りましょう。よければチャンネル登録お願いします。
https://www.youtube.com/watch?v=5r6oygwt-pk&t=0s　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　2-13-1のドップラー効果の振動数公式\(\displaystyle f’=\frac{V-v_o}{V-v_s} f \) の証明方法は何通りかある。一番有名なのは、2-13-1の通り「音源が近づくとき波長は縮む」ことを利用する方法。この単元では2通り目の方法（これも入試では頻出）を扱うが、波長の話は一切出ない証明となる。動画を見れば分かる通り、すでに2通り目の証明としては済んでいる。が、入試でよく出題される形式に従って、あらためてこの単元でいわば「動画の焼き直し」をして説明していくことにする。
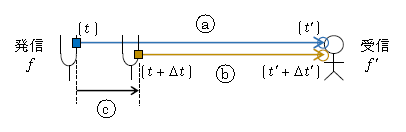
　さて、音源が観測者に近づいている状況を考えよう（図１）。音源(おんさ)が時刻\(t\)に発した音（青い□）が観測者に届く（青い〇）時刻を\(t’\)とする。次に、音源が時刻\(t+\Delta t\)に発した音（黄色の□）が観測者に届く（黄色の〇）時刻を\(t’+\Delta t’\)とする。すると、青い□と黄色の□の時間間隔\(\Delta t\)を「発信間隔」と呼べる。また、青い〇と黄色の〇の間隔\(\Delta t’\)は「受信間隔」と呼べる。

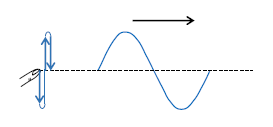
　ここで波の1波長分を「波の数」1個分と数えることにする。例えばひもの端を手でもって上下に1回振動させれば、波1個分が生じる（図２）。ということは、音源の振動数を\(f\)とすると、1sあたり\(f\)回振動しているから、1sあたり波が\(f\)個発せられることになる。発信間隔\(\Delta t\)では発信された波の数は\(f×\Delta t\)個だ。
　同様に、観測者が受信するときの振動数を\(f’\)とすれば、受信間隔\(\Delta t’\)で受信した波の数\(f’×\Delta t’\)個。
　いま、発信した波の数\(f\Delta t \,=\; \)受信した波の数\(f’\Delta t’\) 　　　　 　 (1)
が成り立っている。というのも ―― 例えば図１の青い□で波の山が発せられて、黄色の□で次の次の山が発せられたとするなら、発信された波の数は2個。波の山はその高さを保ちつつ平行移動するのが波動で、青い□の山が観測者に山として届くときが青の〇。次の次の黄色の□の山が観測者に山として届くときが黄色の〇。ならば、観測者の受信した波の数も当然2個。つまり(1)が成り立っているというわけである。
　ということは、\(\Delta t\)と\(\Delta t’\)の関係が分かれば(1)より\(f’\)が求まる。
　そこで、青い矢印や黄色の矢印の距離の関係を調べることにする（図１）。距離は速さ×時間だから、距離の関係から時間\(\Delta t\)と\(\Delta t’\)の関係が得られるはずだ。具体的には、
　青い矢印の距離(a)\(=\)黄色の矢印の距離(b)\(+\)黒い矢印の距離(c)　　(2)
と立式する。音速を\(V\)、音源の速さを\(v\)として、
　(a)\(=V(t’-t)\) 、(b)\(=V(t’+\Delta t’ -(t+\Delta t)) \) 、(c)\(=v(t+\Delta t-t)\)

　これらを(2)に代入すると　\(V(t’-t)=V(t’-t+\Delta t’-\Delta t)+v\Delta t \)
　両辺で\(V(t’-t)\)が打ち消すから、 \(\Delta t’\)について解くと
　　\(V\Delta t’=(V-v)\Delta t \)　　∴　\(\displaystyle \Delta t’=\frac{V-v}{V} \Delta t \)　
　これを(1)に代入して　\(\displaystyle f’\frac{V-v}{V} \Delta t =f\Delta t \)
　よって　\(\displaystyle f’=\frac{V}{V-v} f \)　
　音源が観測者に近づくときのドップラー効果の公式が証明された。
　
　音源が観測者に近づくときのみならず、観測者が音源から遠ざかるときも、音源と観測者の両方が動いているときも、同様の考え方で証明できる。まとめると ―― (1)の「波の数の保存」を念頭に置きつつ、距離の関係を発信間隔\(\Delta t\)と受信間隔\(\Delta t’\)を用いて(2)のように表し、\(\Delta t\)と\(\Delta t’\)の関係を得ればよい。