1-27-2: ベルト上の単振動 ＜例題＞＜動画あり＞

michisanpo – YouTubemichisanpo – YouTubeで関連動画をまず見てから、この単元の実戦演習をしましょう！よければチャンネル登録お願いします。　　
https://www.youtube.com/watch?v=Iz6dIP1_ez8&t=0s

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

例題　

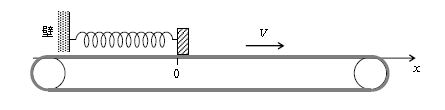
　図のように、弾性定数\(k\)で質量の無視できるばねの一端を壁に取り付けて水平に配置し、他端には質量\(m\)の物体Aをつないで、水平なベルトコンベアの上に置く。水平方向に右向きを正とする\(x\)軸を取り、ばねが自然長のときのAの位置を\(x=0\)とする。いま、Aを\(x=0\)に置いてベルトコンベアを一定速度\(V\)で右回りに動かし始めた。Aとベルトコンベアの間の静止摩擦係数を\(\mu\)、動摩擦係数を\(\mu’\)とし、重力加速度を\(g\)とする。ベルトは十分長くAがベルトから落ちることはない。
問１　Aは位置\(x=x_1\)まではベルトに対して滑ることなく移動する。\(x<x_1\)での摩擦力の大きさ及び\(x_1\)を求めよ。
問２　Aは\(x_1\)を超えるとベルトに対して滑って単振動をする。単振動の中心の座標\(x_0\)及び周期を求めよ。
問３　Aの到達する座標の最大値\(x_2\)及び最小値\(x_3\)を求めよ。
問４　\(x_1\)で単振動が始まった後、Aの速度が次に\(V\)になる位置\(x_4\)でAは再びベルトコンベア上に静止したまま移動するようになる。\(x_4\) を求めよ。

解答・解説

　1-24-1: 単振動の時間変化の調べ方　に基づいて考えていく。
　まず軸と力（図１）　正の向き、原点、自然長の位置、つり合い点を押さえる。つり合い点及び任意の\(x\)に物体を書く。
　ここでは、つり合いに2種類あることに気付きたい。1種類目は、静止摩擦\(R\)が働きながらのつり合い（図１a）。物体がベルトと同速\(V\)で動き出すと、摩擦は接触面どうし(上の物体と下のベルト)が滑り合うのを妨げようとするから、ベルトに物体をくっ付き合わせながら等速度運動させようとする。物体が右へ行き、ばねの伸びが増え、左向きの弾性力=\(k\)×伸び \(x\)が増えるほど、滑りを妨げる右向きの静止摩擦\(R\) ―― 接触面(下の面)から見て物体が静止中の摩擦力 ―― が大きくなり、「力がつり合うと物体は等速」(運動の第１法則）となる。
　\(\displaystyle\)こうして静止摩擦\(R\)が大きくなっていくと、やがて\(x=x_1\)にて\(R=\)最大摩擦\(\mu N\)（図１a）に達する。最大摩擦に達した次の瞬間には、摩擦の大きさが動摩擦\(\mu’ N\)にガクンと減る(1-09-1)。この動摩擦中のつり合いが2種類目のつり合いだ（図１b）。摩擦は接触面どうし(上の物体と下のベルト)が滑り合うのを妨げようとするから、ベルトが右へ行くと、ベルトに物体をくっ付かせようとするべく、右向きに動摩擦が働く。物体がＵターンして左向きへ移動しているときも、ベルトは相変わらず右へ行くから、ベルトに物体をくっ付かせようとするべく右向きに動摩擦が働く。

　次に\(ma=F\)　　
問１　\(x\)でのつり合い（図１a）: \(0=-kx+R\)　　∴　\(R=\)　答　\(kx\)
　　特にベルトに対して物体が滑り出す直前\(x₌x_1\)では、最大摩擦\(\mu N=\mu mg\)を用いて、
　　\(x_1\)でのつり合い: \(0=-kx_1+\mu mg\)　　∴　\(x_1=\)　答　\(\displaystyle \frac{\mu mg}{k} \)
　　ついでに、動摩擦中のつり合い（図１b)：\(0=-kx_c+\mu’ mg\)　　∴　\(\displaystyle x_c=\frac{\mu’ mg}{k} \)
問２　動摩擦が働いているときの任意の\(x\)の図は図1cに示した。
　　 任意の\(x\)の運動方程式（図１c)：\(\displaystyle ma=-kx+\mu’ mg　=-k \left(x-\frac{\mu’ mg}{k}\right )\)　　(☆)
　　　∴　\(\displaystyle a=\frac{d^2x}{dt^2}=-\frac{k}{m} \left(x-\frac{\mu’ mg}{k} \right) \)
　　　　　　　 \(\displaystyle\)\(\displaystyle \frac{d^2x}{dt^2}=-\:〇\:(x-　□　)\) (単振動の方程式)と比べて
　　〇\(\displaystyle=\omega^2=\frac{k}{m} \) 、□\(=\)中心\(x_0=\)　答　\(\displaystyle \frac{\mu’ mg}{k}\)　と分かる（つり合い点 \(x_c\)と中心 \(x_0\)が一致しているのは1-23-1でやった通り）。
　　周期\(\displaystyle T=\frac{2\pi}{\omega} =\)　答　\(\displaystyle 2\pi\sqrt{\frac{m}{k}} \)

　運動\(v,x\)を調べる
問３　\(x\)の最大値及び最小値を調べたいのであれば、これは明らかに振動中の両端の点で\(v=0\)になる所(1-18-1)、しかも\(v=0\)になるまでの時間を求めなくてよいからエネルギー保存則を用いるのがピッタリだ。（ 1-24-2: 単振動の\(x\)-\(t\)グラフの4パターン　に当てはまっていないので、1-24-2のように直接 \(x=\pm A\sin \omega t\), \(\pm A\cos \omega t\)とは表せないという事情もある。というのも、\(x_1\)という中心\(x_c\)とは異なる位置で単振動が始まっているし、しかもそのときの初速\(V\neq 0\)だから。）よってエネルギー保存則で行こう。
　さて、1-26-1より、運動方程式(☆)が
　　\(\displaystyle ma=-k(x-x_c)\)　[ ただし\(\displaystyle x_c=\frac{\mu’ mg}{k} \) ]　の形だから、
　エネルギー保存則は　\(\displaystyle \frac{m}{2}v^2+ \frac{k}{2}(x-x_c)^2=\)一定　となる。　
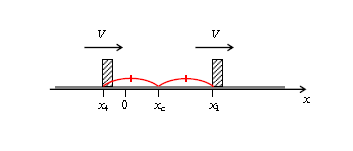
　これを単振動の開始点\(x_1\)と求める\(x’=x_2\)または\(x_3\)について立てると（図２）、
　　\(\displaystyle \frac{m}{2}V^2+ \frac{k}{2}(x_1-x_c)^2=\frac{m}{2}0^2+ \frac{k}{2}(x’-x_c)^2\)　　(＊)
　　\(\displaystyle\)∴　\(\displaystyle (x’-x_c)^2=\frac{mV^2}{k}+ (x_1-x_c)^2\)
　　\(\displaystyle\)∴　 \(\displaystyle x’=x_c\pm \sqrt{\frac{mV^2}{k}+ (x_1-x_c)^2} \)
　　\(x_2>x_3\)だから、\(x’=x_c\pm \cdots \) のうち、\(+\)の方の解が\(x_2\)、\(-\)の方の解が\(x_3\)。
　　よって \(\displaystyle\) \(x_2=\)　答　\(\displaystyle\frac{\mu’ mg}{k}+\sqrt{\frac{mV^2}{k}+ \left((\mu -\mu’)\frac{mg}{k} \right)^2}\)
　　　　　\(\displaystyle\) \(x_3=\)　答　\(\displaystyle\frac{\mu’ mg}{k}-\sqrt{\frac{mV^2}{k}+ \left((\mu -\mu’)\frac{mg}{k} \right)^2}\)
　[ ちなみに、動摩擦がからむと摩擦熱が発生するから、摩擦熱エネルギーの分、力学的エネルギー(運動エネルギーと位置エネルギーの和)は減少する。しかし熱エネルギーの分まで含めて、熱＋力学的エネルギーの合計を取ると、エネルギーは一定値を取る（自然界のエネルギーは力学的・熱・電気・光・原子力・…全てひっくるめると保存する）。(＊)はそういった意味の式である。単振動という現象を扱う限り、とにもかくにもエネルギー保存則が(＊)の形で書けることは1-26-1で説明した通り。 ]

問４　いま、ある距離\(l\)について\(x=x_c+l\)での速さ\(v_+\)と、\(x=x_c-l\)での\(v_-\)を比べることにしたい。単振動独特のエネルギー保存則
　　\(\displaystyle \frac{m}{2}v^2+ \frac{k}{2}(x-x_c)^2=\)一定
を用いると、
　　\(\displaystyle \frac{m}{2}v_+^2+ \frac{k}{2}k(x_c+l-x_c)^2=\frac{m}{2}v_-^2+ \frac{k}{2}(x_c-l-x_c)^2\)
　形式上の弾性エネルギー\(\frac{k}{2}(\cdots)^2\)の項が左辺と右辺でともに\(\frac{k}{2}l^2\)と等しいから、\(\frac{m}{2}v_+^2=\frac{m}{2}v_-^2\) すなわち\(v_+=v_-\)であることが分かる。つまり、単振動では中心\(x_c\)から右へある距離ずれたときの速さと左へ等しい距離ずれたときの速さが等しい。これを単振動の中心対称性という（ちなみに1-15-3では等加速度直線運動の対称性を扱った）。
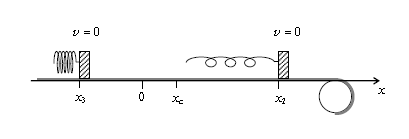
　ということは、位置\(x_1\)での速度が右向きに\(V\)であったことから、同様に右向きに\(V\)になる位置\(x_4\)は、中点公式を用いて（図３）　\(\displaystyle \frac{x_1+x_4}{2}=x_c \)
　∴　\(\displaystyle x_4=2x_c-x_1=\frac{2\mu’ mg}{k}-\frac{\mu mg}{k}=\)　答　\(\displaystyle (2\mu’-\mu)\frac{mg}{k}\)