1-17-2: 力学的エネルギーの変化
力学的エネルギーは保存するだけでなく、変化する場合があるので注意しましょう! → <例題>は1-17-3 へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 重力・弾性力(保存力)以外が仕事をすると、力学的エネルギーは保存しない
力学的エネルギー変化 = 重力・弾性力(保存力)以外のした仕事
力学的エネルギーが保存しない例として、図1のように物体が壁に沿って動摩擦力\(R\)を受けながら落下する場合を考察する。1-16-1でやった
(運動エネルギー変化=仕事)つまり
\(\displaystyle \frac{m}{2} v^2- \frac{m}{2} {v_0}^2 =W \) (1)
を用いる。
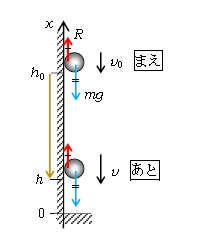
力が2本あるので、仕事も動摩擦のした仕事\(W_R\)と重力のした仕事\(W_g\)の2本分を計算する。
仕事\(W\)=(力の移動方向成分)×(距離)
だが、物体の移動方向が下向きなのに対して動摩擦は上向き(逆向き)だから、動摩擦の移動方向成分は\(+R\)ではなく\(-R\)であることに注意。
ゆえに\(W_R=-R×(h_0-h) \)(1-16-1でやった通り、力の向きと移動の向きが逆ならば仕事は負)
一方、\(W_g=mg×(h_0-h)=mgh_0-mgh \)
すると(1)式より
\(\displaystyle \frac{m}{2} v^2- \frac{m}{2} {v_0}^2 =W_g+W_R=mgh_0-mgh-R(h_0-h) \)
∴ \(\displaystyle \left(\frac{m}{2} v^2 +mgh \right) – \left(\frac{m}{2} {v_0}^2 +mgh_0 \right) =-R(h_0-h) \) (2)
ここで図1より、\(\displaystyle \frac{m}{2} v^2 +mgh\)=あとの力学的エネルギー
\(\displaystyle \frac{m}{2} {v_0}^2 +mgh_0 \)=まえの力学的エネルギー だから、
(2)の左辺=(あとの力学的エネルギー)-(まえの力学的エネルギー)
=力学的エネルギー変化
一方、(2)の右辺=動摩擦\(R\)のした仕事
ゆえに(2)は「力学的エネルギー変化=動摩擦\(R\)のした仕事」となる。
(2)の右辺\(\ne \)0だから、左辺\(\ne \)0、つまり 変化=あと-まえ\(\ne \)0、つまり あと\(\ne \)まえ。よって、動摩擦力\(R\)が仕事をすると力学的エネルギーは保存しない。
仕事をしても力学的エネルギー保存が成り立つ力を「保存力」という。代表的な保存力は重力と弾性力である。仕事をすると力学的エネルギーを変化させる力は「非保存力」という。代表的な非保存力は動摩擦力である。
最後に、この単元では証明しないが重要な結論を2つまとめておこう。
1⃣ 重力・弾性力(保存力)のみが仕事をするときには力学的エネルギーは保存する。
2⃣ 動摩擦力はもちろんのこと、重力・弾性力(保存力)以外の力が仕事をすると、その分だけ力学的エネルギーは変化して保存しない。
力学的エネルギー変化 = 重力・弾性力(保存力)以外のした仕事
以上の証明を学習したい人は10-04-1にきっちりとした説明が載っている(10-04-1を読む前準備として、1-16-2,1-16-3,10-03-1,10-03-2を学習しておかねばならないが)。興味のある人は参考にしてほしい。なお、(その証明は抜きにして)弾性力が関わる場合の力学的エネルギー保存則は次の1-18-1で扱う。
→ <例題>は1-17-3 へ


