1-16-2: 2次元の運動エネルギーと仕事
この単元が難しすぎると感じたなら、飛ばして1-17-1に行けば差し当たり問題なしです。しばらくしたらこの単元にまた戻ってきましょう。 → <続き>は1-16-3へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 加速度 \(\displaystyle \vec{a}=\lim_{\Delta t → 0} \frac{\Delta\vec{v}}{\Delta t}=\frac{d\vec{v}}{dt} \)
速度 \(\displaystyle \vec{v}=\lim_{\Delta t → 0} \frac{\Delta\vec{r}}{\Delta t}=\frac{d\vec{r}}{dt} \) (\(\Delta \vec{r}\): 変位(ベクトル))
・ 運動エネルギー\(\displaystyle K=\frac{m}{2}|\vec{v}|^2 \) (\(m\): 質量)として
\(\displaystyle \Delta \left( \frac{m}{2}|\vec{v}|^2 \right) =|\vec{F}|\cos\phi \cdot |\Delta \vec{r}| \) (ただし\(\Delta \vec{r}→ \vec{0}\)で、\(\phi\)は\(\vec{F}\)と\(\Delta \vec{r}\)のなす角)
この単元では、数学の微分及び内積
\(\vec{a}\cdot\vec{b}=a_xb_x+a_yb_y=|\vec{a}||\vec{b}|\cos\phi \)(\(\phi\)は\(\vec{a}\)と\(\vec{b}\)のなす角) (☆)
が(まやかしでない)説明には必要になる。この単元と次の1-16-3をしっかり勉強すれば、物理の面白さにあらためて気付く人も多いと思う。一方、微分や内積を習っていない人でも、次の1-16-3のポイントと図を見ておくのは役に立つだろう。
準備として、2次元運動における加速度\(\vec{a}\)の説明しておこう。1-02-1の通り加速度とは1sあたりの速度変化で、2次元での速度変化は\(\Delta\vec{v}\)だから
加速度 \(\displaystyle \vec{a}=\frac{\Delta\vec{v}}{\Delta t} \) (ただし\(\Delta t→0\))
つまり \(\displaystyle \vec{a}=\lim_{\Delta t→0} \frac{\Delta\vec{v}}{\Delta t}=\frac{d\vec{v}}{dt} \) (1)
[ 微分で \(\displaystyle \frac{d \,〇}{dt} \) のように書かれていたら、
心の中では \(\displaystyle \frac{\Delta \,〇}{\Delta t} \)(ただし\(\Delta t→ 0\))と読むのをおすすめする。すると、「1sあたりの 〇 の変化」のように意味がつかみやすい。 (*) ]
さて、\(\Delta \vec{v}=(\Delta v_x \, , \, \Delta v_y)\) のように成分表示できるから、(1)より
\(\displaystyle \vec{a}=\left( \lim_{\Delta t→0} \frac{\Delta v_x }{\Delta t} \, , \, \lim_{\Delta t →0} \frac{\Delta v_y }{\Delta t} \right) =\left( \frac{dv_x }{dt} \, , \, \frac{dv_y }{dt} \right) \)
つまり \(\displaystyle a_x=\frac{dv_x }{dt} \, , \, a_y=\frac{dv_y }{dt} \)
ということは(*)より、加速度の\(x\)成分\(a_x\)とは1sあたりの\(v_x\)の変化である。ところで1-15-1の通り\(v_x\)とは「\(x\)軸方向に沿う速度」だから、\(a_x\)とは「\(x\)軸方向に沿う加速度」とも言える。
(1)を用いて運動方程式\(m\vec{a}=\vec{F} \)は \(\displaystyle m\frac{d\vec{v}}{dt}=\vec{F} \) と書ける。 (2)
では運動エネルギーの話に移ろう。まず運動エネルギーを1文字\(K\)で表し、\(\displaystyle K=\frac{m}{2}|\vec{v}|^2 \)\(\displaystyle =\frac{m}{2}({v_x}^2+{v_y}^2) \) と定義(1-02-1)する。次に、単元タイトルの運動エネルギーと仕事の関係を導くために、\(K\)を時間\(t\)で微分してみる。 [ なぜか。こうするとゆくゆくは上手く行くから微分するので、なぜ微分?と手を止めたりせず、話に付いてくることが大切 ]
\(\displaystyle \frac{dK}{dt} = \frac{d (\frac{m}{2}({v_x}^2+{v_y}^2) )}{dt} =\frac{d (\frac{m}{2}{v_x}^2) }{dt}+\frac{d (\frac{m}{2}{v_y}^2) }{dt} \)
\(\displaystyle =\frac{d (\frac{m}{2}{v_x}^2) }{dv_x} \frac{dv_x}{dt}+\frac{d (\frac{m}{2}{v_y}^2) }{dv_y} \frac{dv_y}{dt} \) [ つまり合成関数の微分を用いている ]
\(\displaystyle =mv_x \frac{dv_x}{dt}+mv_y \frac{dv_y}{dt} =m \left( \frac{dv_x}{dt}v_x+ \frac{dv_y}{dt}v_y \right) \) [ ここで(☆)を使う ]
\(\displaystyle =m\frac{d\vec{v}}{dt} \cdot \vec{v} \) さらに(2)を用いると、一区切りの式
\(\displaystyle \frac{dK}{dt} =\vec{F} \cdot \vec{v} \) (3)
が得られる。右辺には「仕事率」という名前が付いている(が、ここでは深入りしない)。
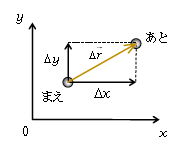
ところで、1次元運動での変位\(\Delta x\)に\(\Delta y\)を組合わせたものを変位ベクトル(あるいは単に変位)\(\Delta \vec{r}=(\Delta x \, , \, \Delta y)\)という(図1)。まさにまえからあとへの位置の変化を表したもの。すると、
速度 \(\displaystyle \vec{v}=\lim_{\Delta t \rightarrow 0} \frac{\Delta\vec{r}}{\Delta t}=\frac{d\vec{r}}{dt} \) [ (*)より1sあたりの位置の変化という意味 ]
これを(3)に代入すると \(\displaystyle \frac{dK}{dt} =\vec{F} \cdot \frac{d \vec{r}}{dt} \)
すなわち \(\displaystyle \frac{\Delta K}{\Delta t} =\vec{F} \cdot \frac{\Delta \vec{r}}{\Delta t} \) (ただし\(\Delta t→ 0\))
分母の\(\Delta t\)を払い、左辺に\(K=\frac{m}{2} |\vec{v}|^2 \)を代入すると
\(\displaystyle \Delta \left( \frac{m}{2}|\vec{v}|^2 \right) =\vec{F} \cdot \Delta \vec{r} \) 右辺に(☆)を用いると
\(\displaystyle \Delta \left( \frac{m}{2}|\vec{v}|^2 \right) =|\vec{F}|\cos\phi \cdot |\Delta \vec{r}| \)(ただし、\(\Delta t→ 0\)だから\(\Delta \vec{r}→ \vec{0}\) 。また\(\phi\)は\(\vec{F}\)と\(\Delta \vec{r}\)のなす角)
これが我々の得たかった式である。これを用いて、次の単元1-16-3の話を展開していく。