10-03-2: 位置エネルギー

位置エネルギーの本格的な説明をします！　　→　関連事項は10-03-1: 保存力、10-04-1: 力学的エネルギー保存則の証明 へ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　このトピックの狙いは位置エネルギーをしっかりと定式化すること。そのために数学の区分求積法
　　\(\displaystyle \lim_{\Delta x→0}\sum_{k=1}^{n} f(x_k) \Delta x = \int_a^b f(x)dx \)　　を用いる。
　では2次元の運動エネルギーと仕事の関係
　運動エネルギー変化 ＝　仕事　　　から始める。
　\(\displaystyle \frac{m}{2}|\vec{v}|^2- \frac{m}{2}|\vec{v_0}|^2 \) \(=\)　\(\displaystyle W=\lim_{\Delta \vec{r}→\vec{0}} \sum_{\Delta \vec{r}} |\vec{F}|\cos\phi \cdot |\Delta \vec{r}| \)
（この式の導出・説明は1-16-2,1-16-3を、右辺の仕事\(W\)の手短かな説明は10-03-1を参照してほしい。）
　まず内積を用いて、右辺の\(|\vec{F}|\cos\phi \cdot |\Delta \vec{r}|= \vec{F}\cdot \Delta \vec{r} \) と書き換えると
　　\(\displaystyle W=\lim_{\Delta \vec{r}→\vec{0}} \sum_{\Delta \vec{r}} \vec{F}\cdot \Delta \vec{r} \)
　次に区分求積法を用いれば \(\displaystyle \lim_{\Delta 〇→0} \sum \cdots \Delta 〇=\int \cdots d〇 \) のようになるから、
　\(\displaystyle W=\int_C \vec{F}\cdot d\vec{r} \)　　　　　　　　　　　　　　　　　　　　(1)
　\(\int\)の右下の記号\(C\)はcurveといった意味で、「この積分をある特定の経路\(C\)（たとえば放物軌道）に沿って行いなさい」と経路を指定する記号である。
　また、原点Oから点(\(x,y\))へ向くベクトルとして位置ベクトル(あるいは単に位置)\(\vec{r}\)を導入しておく（図１）。\(\vec{r}\)の変化量\(\Delta \vec{r}\)は変位に他ならない。

　さて、\(x\)の関数\(f(x)\)と同様の記号で、位置\(\vec{r}\)での保存力による位置エネルギーを\(U(\vec{r})\)と表すと、定義により
　\(U(\vec{r})=\)ある位置\(\vec{r}\)から基準点\(\vec{r_0}\)まで
　　　　　保存力\(\vec{F_保}\)がすることのできる仕事\(W(\vec{r}→\vec{r_0}) \: \)　　 (2)
である。1-17-1の重力による位置エネルギーは「高さ\(h\)から高さ0の所(基準点)まで重力がすることのできる仕事」(すなわち\(mgh\))、1-18-1の弾性力による位置エネルギーは「のび・ちぢみ\(|x|\)から自然長の位置(基準点)まで弾性力がすることのできる仕事」。このように、位置エネルギーの平たい意味は「仕事する能力」である（ちなみに位置エネルギーの英語はpotential energyでpotentialの直訳は潜在能力）。10-03-1の通り、保存力では始めの位置\(\vec{r}\)と終りの位置\(\vec{r_0}\)だけで仕事\(W(\vec{r}→\vec{r_0})\)の値が決まってしまい、その値が途中の移動経路しだいで変わらないから、(2)によって位置エネルギーを一意に定義できる。
　ここで(1)の積分を、(2)の\(W(\vec{r}→\vec{r_0})\)（\(\vec{r}\)から\(\vec{r_0}\)までの仕事）に適用する。積分区間は\(\vec{r}\)(下端)から\(\vec{r_0}\)(上端)までであることに注意して、
　\(\displaystyle U(\vec{r})=\int_{\vec{r}}^{\vec{r_0}} \vec{F_保}\cdot d\vec{r}\)　　　　　　　　　　　　　　　　　　(3)
保存力\(\vec{F_保}\)についてはこの積分値(仕事)は経路しだいで変わらないから、(1)のような経路指定の記号\(C\)は不要である。

　こうして位置エネルギーが定式化されると、「位置エネルギーと仕事の関係」が得られる。それは
　位置エネルギーのまえーあと　＝　まえからあとで保存力のする仕事
　　　　\(U_{まえ}-U_{あと}\)　　　　 \(=\)　　　\(W(まえ→あと) \)　　　(4)
これを証明しよう。まえとあとの位置をそれぞれ\(\vec{r_{1}} \, 、\vec{r_{2}} \)とすれば、
　\(U_{まえ}-U_{あと}=U(\vec{r_{1}})-U(\vec{r_{2}})\)　　[ (3)を代入 ]
　　\(\displaystyle =\int_{\vec{r_1}}^{\vec{r_0}} \vec{F_保}\cdot d\vec{r} \; – \int_{\vec{r_2}}^{\vec{r_0}} \vec{F_保}\cdot d\vec{r} \)　　[ 第2項の上端・下端をひっくり返して ]
　　\(\displaystyle =\int_{\vec{r_1}}^{\vec{r_0}} \vec{F_保}\cdot d\vec{r} + \int_{\vec{r_0}}^{\vec{r_2}} \vec{F_保}\cdot d\vec{r} \)　　[ \(\displaystyle \int_{\vec{r_1}}^{\vec{r_0}} + \int_{\vec{r_0}}^{\vec{r_2}} = \int_{\vec{r_1}}^{\vec{r_2}} \) だから ]
　　\(\displaystyle =\int_{\vec{r_1}}^{\vec{r_2}} \vec{F_保}\cdot d\vec{r} \)　　[ (1)を用いて ]
　　\(=W(r_{1} →r_{2})=W(まえ→あと) \)　　　よって(4)が証明された。
　力学の他の法則「運動エネルギー変化(あとーまえ)＝まえからあとでの仕事」や「運動量変化(あとーまえ)＝まえからあとでの力積」と違って、「位置エネルギー(まえーあと)=まえからあとでの保存力の仕事」となっていることに注意しよう。

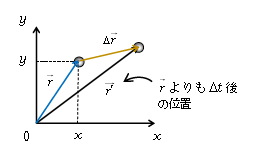
　この位置エネルギーと仕事の関係の例として、重力の場合を説明しておく。図２に高さ\(h\)のまえ状態から\(h’\)のあと状態への移動が示してある。まえの位置エネルギーは\(mgh\)で、まえは仕事する能力が\(mgh\)あるという意味。あとの位置エネルギーは\(mgh’\)で、あとは仕事する能力が\(mgh’\)。位置エネルギー(まえーあと)は位置エネルギーの減少量\(mg(h-h’)\)で、すなわち仕事する能力の減少量。一方、まえからあとでの重力の仕事\(＝mg\)×(高さの減少分)(10-03-1を参照）\(=mg(h-h’)\) 。よって確かに(4)が成り立っている。
　このように、重力が仕事をするとその分だけ仕事する能力(位置エネルギー)が減っている。お金にたとえて、お金を3000円使うとその分お金を使う能力が減る、のように理解するのも悪くない。(4)はそのようなことを保存力一般について言っている式である。