1-17-3: 力学的エネルギーの保存と変化 ＜例題＞

力学的エネルギーが保存する場合と変化する場合を、きっちりと区別しましょう！　　　　　　　　　　　　　

例題　

　図１のように、斜面S₀、S₁と水平な床がなめらかにつながっている。斜面S₀および床は摩擦のない面であり、斜面S₁は粗い面である。床から高さ\(h\)の斜面S₀上の点Pより、質量\(m\)の小物体Aを斜面に沿って下方に速さ\(v_0\)で打ち出した。ただし、斜面S₁の水平面からの角度を\(\theta\)とし、重力加速度の大きさは\(g\)とする。また、斜面S₁と小物体A の間の動摩擦係数を\(\mu '\)とする。

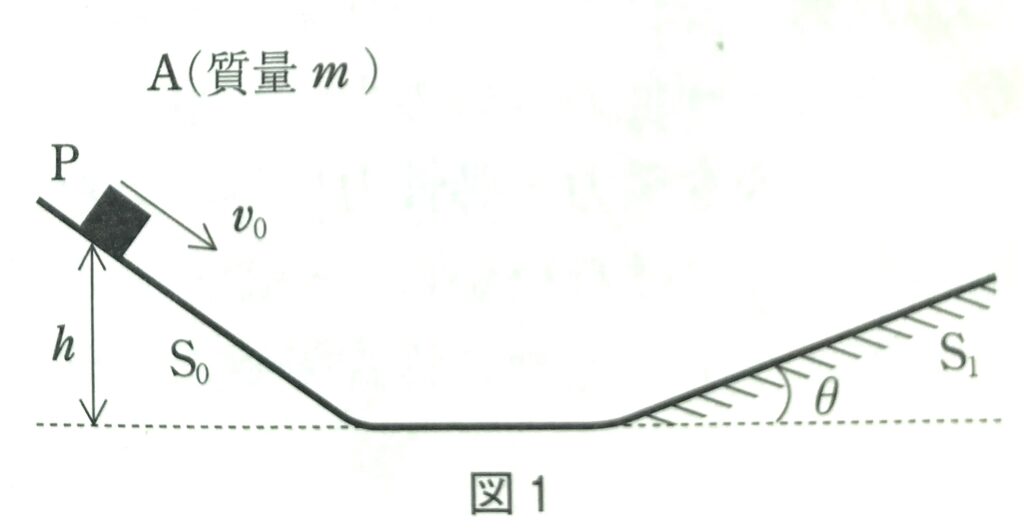
問１　床での小物体の速さはどれだけか。正しいものを、次の①～⑥のうちから一つ選べ。
①　\(v_0+\sqrt{gh} \)　　②　\(\sqrt{{v_0}^2-gh} \)　　③　\(\sqrt{{v_0}^2-2gh} \) 　
④　\(v_0+\sqrt{2gh} \)　　⑤　\(\sqrt{{v_0}^2+gh} \)　　⑥　\(\sqrt{{v_0}^2+2gh} \)　
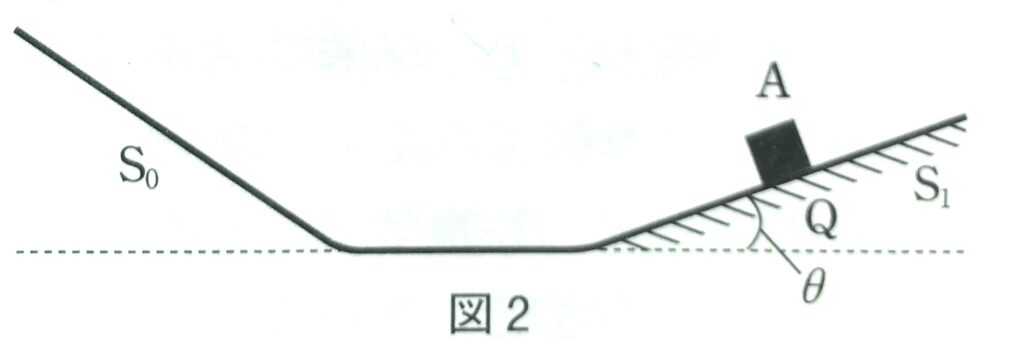
問２　図２のように、小物体Aは斜面S₁をのぼり、点Qにおいて速さが0になった。重力による位置エネルギーの基準を床に取ると、小物体の点Qでの位置エネルギーは床での運動エネルギーの何倍か。正しいものを、次の①～⑥のうちから一つ選べ。
①　\(\displaystyle \frac{1}{\sin\theta +\mu '\cos\theta} \)　　②　\(\displaystyle \frac{1}{\cos\theta +\mu '\sin\theta} \)　　
③　\(\displaystyle \frac{\cos\theta}{\sin\theta +\mu '\cos\theta} \) 　④　\(\displaystyle \frac{\cos\theta}{\cos\theta +\mu '\sin\theta} \)　　
⑤　\(\displaystyle \frac{\sin\theta}{\sin\theta +\mu '\cos\theta} \)　　⑥　\(\displaystyle \frac{\sin\theta}{\cos\theta +\mu '\sin\theta} \)

解答・解説

　問１は、単に速さを求める、時間を求めなくてよい問題なので、1-17-1の通りエネルギーを用いる。問２は問題文からしてもちろんエネルギー。ところで、1-17-2でやった通り
１⃣　重力・弾性力のみが仕事をするときには力学的エネルギー保存
２⃣　重力・弾性力以外の力が仕事をすると力学的エネルギー変化
いずれの場合も重力・弾性力以外の力が働いているかどうか、しっかりと見極めないといけないから、やはり力は書き込む。力学の問題は、エネルギーで解こうが、運動方程式で解こうが、力は図示するのだ。

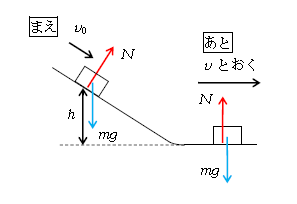
問１　重力・弾性力以外の力は\(N\)（図３）。力\(N\)は物体の移動方向（斜面平行方向や水平方向）と垂直だから、\(N\)の移動方向成分は0、つまり\(N\)の仕事=(\(N\)の移動方向成分)×(距離)=0。これが1-16-1で述べた「力の向きと移動の向きが垂直ならば仕事は0」である。重力・弾性力以外の力\(N\)が仕事しないから、
１⃣　力学的エネルギー保存　を用いる。
　エネルギー保存は　あと　　=　　まえ　　　　と立てる（図３）。
　　　　　　　\(\displaystyle \frac{m}{2} v^2+mg0= \frac{m}{2} v_0^2 +mgh \)
　∴　\(v^2={v_0}^2+2gh \)　　∴　\(v=\sqrt{{v_0}^2+2gh} \)　　　　　答　⑥

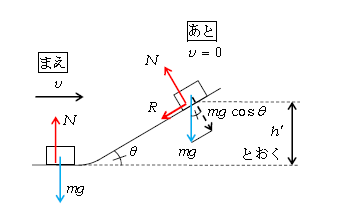
問２　重力・弾性力以外の力は\(N\)と動摩擦力\(R\)（図４）。
　問１と同様に\(N\)の仕事は0だが、動摩擦が仕事をする から、
２⃣　力学的エネルギー変化=重力・弾性力以外の仕事=動摩擦の仕事\(W_R\)　を用いる。
　力学的エネルギー変化は　あと　　－　　まえ　　　と立てる（図４）。
　　　　　　　　\(\displaystyle \left(\frac{m}{2}0^2+mgh’ \right) – \left(\frac{m}{2} v^2 +mg0 \right) =W_R \)　　(1)

　ということで、\(W_R\)を計算すればよい。
　\(W_R\)=(\(R\)の移動方向成分)×(距離) 　　　　　　　　　　　　　　　(2)　
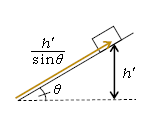
　ここで(距離)とは、\(R\)の加わっている間の距離のことだから、図５より (距離)=\(\displaystyle \frac{h’}{\sin\theta} \)。
　また、移動の向きが斜面平行上向きなのに対して、\(R\)の向きはすべり上がるのを妨げる斜面平行下向き（図４）だから、(\(R\)の移動方向成分)=\(-R\)。公式\(R=\mu ' N\)により、\(-R=-\mu ' N\)。

　ところで斜面垂直方向の運動方程式は図４より \(0=N-mg\cos\theta \)　　
　すなわち\(N=mg\cos\theta \) を代入して、結局(\(R\)の移動方向成分) =\(-\mu ' mg\cos\theta \)
　　[ 選択肢中では使えない\(N\)を消去。選択肢を意識しながら、式変形しよう ]
　したがって(2)より　\(\displaystyle W_R=-\mu ' mg\cos\theta ×\frac{h’}{\sin\theta} \)
　これを(1)に代入して 　\(\displaystyle mgh’-\frac{m}{2} v^2 =-\mu ' mg \frac{\cos\theta}
{\sin\theta}h’ \)
　左辺に位置エネルギー\(mgh’\)、右辺に運動エネルギー\(\frac{m}{2} v^2\)と整理し、
　　\(\displaystyle mgh’ \left( 1+\mu ' \frac{\cos\theta}{\sin\theta} \right) =\frac{m}{2} v^2 \)
　　∴　\( \displaystyle mgh’ \frac{\sin\theta +\mu ' \cos\theta}{\sin\theta} =\frac{m}{2} v^2 \)
　　∴　\( \displaystyle mgh’=\frac{\sin\theta}{\sin\theta +\mu ' \cos\theta} ×\frac{m}{2} v^2
\)　　　　　答　⑤