1-18-1: 弾性力と力学的エネルギー保存則
力学的エネルギー保存則を用いて弾性力の下での運動を調べる方法を、しっかり身に付けましょう! → <例題>は1-18-2へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 弾性力による位置エネルギー(弾性エネルギー)
\(\displaystyle =\frac{k}{2} \)×(のび・ちぢみ)\(^2\) [J] (\(k\): ばね定数)
・ 力の移動方向成分を(\(F\cos\theta \)ではなく単に)\(F\)、位置を\(x\)として、
\(F\)-\(x\)グラフの面積=仕事
ばねに対してエネルギーの考え方を用いてみよう。1-17-1で
重力による位置エネルギー=基準点まで重力がすることのできる仕事
と定義した。今度は、
弾性力による位置エネルギー(または弾性エネルギー)=のび・ちぢみ\(|x|\)から
基準点(自然長の位置\(x=0\))まで弾性力が物体にすることのできる仕事 (*)
と定義する。
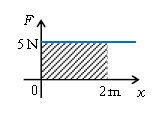
さて、\(F\)-\(x\)グラフが図1のような場合、
\(F\)-\(x\)グラフの面積=5N×2m=(力の移動方向成分)×(距離)=仕事。
つまり、力の移動方向成分(\(F\)とする)が一定なら、\(F\)-\(x\)グラフの面積=仕事 が成り立つ。
しかし、1-14-1でやった通り、弾性力\(F=-kx\)は一定ではない(図2の青線のグラフ)。そこで、1-02-1で \(v\)-\(t\)グラフの面積=変位 を証明するときに用いた、階段グラフの方法を使おう。
横軸の\(x~0\)を\(\Delta x \)ごとに区切って、\(F\)が階段状に変化していくとする。図2では5等分したが、最終的には無限個等分し、階段グラフを\(F=-kx\)のグラフに限りなく近づける。
まず、長方形aにおいては(力の移動方向成分、すなわち移動の向き左向きを正とする成分)=\(|F|\)=長方形のタテの長さ が一定だから、
\(F\)-\(x\)グラフの面積=仕事
が成り立つ。これが階段グラフを用いるメリットで、aの面積は最初の\(\Delta x\)での仕事に等しい。
同様に、bの面積は次の\(\Delta x\)での仕事に等しい、・・・。
全ての長方形を足した階段グラフの面積は、\(x~0\)での仕事の合計に等しい。したがって\(x~0\)の\(F\)-\(x\)グラフの面積=\(x~0\)での仕事 となる。
ところが(*)より、これは弾性エネルギーに他ならない。
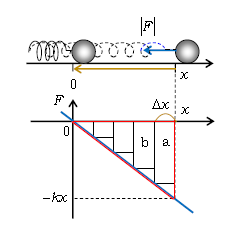
よって、弾性力による位置エネルギー=\(x~0\)の\(F\)-\(x\)グラフの面積
=図2の赤の直角三角形の面積=\(\displaystyle x\cdot kx \cdot \frac{1}{2}\)\(\displaystyle =\frac{k}{2} x^2 \)
図2では\(|x|\)がばねののびを表すが、ちぢみの場合も同じ結論\(\frac{k}{2} x^2 \)となる。[ なお、いまの場合移動の向き(左向き)と\(F\)の向き(左向き)は同じだから、\(F\)の移動方向成分はプラスとなり、\(x~0\)での仕事はプラス、ゆえに(*)より弾性エネルギーもプラスで、\(-\frac{k}{2} x^2 \)のようにはならない。]
さらに、力の移動方向成分\(F\)が変化していく場合、\(F\)-\(x\)グラフの面積=仕事 が成り立つことも言えた。ただし、[ ] の中で述べたことから分かる通り、「横軸の下側の\(v\)-\(t\)グラフの面積は負の値である」(1-02-1)のような取り決めは通用せず、力の向きと移動の向きが同じか逆かに応じて\(F\)-\(x\)グラフの面積も正か負(1-16-1)になる。
単位を確認しておこう。1-14-1で\(k\)の単位は[N/m]だと述べた。弾性エネルギー\(\frac{k}{2} x^2 \)の単位は[(N/m)\(\cdot \)m\(^2\)=N\(\cdot \)m=J] 。仕事やエネルギーの単位は全て[J]だ。
さて、弾性力による位置エネルギーを定義すると、例えば図3のような弾性力による運動で以下が成り立つ(ここでは証明を略するが、証明に興味のある人は10-04-1を参照するとよい)。
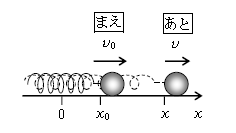
力学的エネルギー保存則、つまり
あとの運エネ + 位エネ = まえの運エネ + 位エネ つまり
\(\displaystyle \frac{m}{2} v^2 \; \) + \(\displaystyle \: \frac{k}{2} x^2 \; \) = \(\displaystyle \frac{m}{2} {v_0}^2 \) + \(\displaystyle \: \frac{k}{2} {x_0}^2 \) (✩)
これを用いて、入試でよく扱われる以下の量を求めよう。
1⃣ のび・ちぢみの最大値
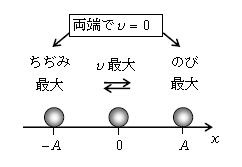
(✩)の右辺は一定値だから、左辺も一定。ゆえに、弾性エネルギー\(\frac{k}{2} x^2 \)が増えるほど、運動エネルギー\(\frac{m}{2} v^2\)は減る。言いかえると、のび\(|x|\)やちぢみ\(|x|\)が大きくなるほど、速さ\(v\)は小さくなる(例えばのび\(|x|\)が大きくなるほど、伸びたばねが小球を左向きに引張る弾性力\(|F|=k|x|\)が大きくなり(図3)、右向き移動中の小球が左向きの力を受けて、速さ\(v\)が小さくなる)。やがて\(v=0\)になっていったん止まったときにのびやちぢみは最大になり、この最大値を振幅\(A\)という。
のびちぢみが最大のときは\(v=0\)だから、(✩)より
\(\displaystyle \frac{m}{2} 0^2 +\frac{k}{2} A^2 =\frac{m}{2} {v_0}^2 +\frac{k}{2} {x_0}^2\)
両辺を\(\displaystyle \frac{2}{k} \)倍して \(\displaystyle A^2 =\frac{m}{k} {v_0}^2 +{x_0}^2 \)
∴ \(\displaystyle A=\sqrt{\frac{m}{k} {v_0}^2 +{x_0}^2} \)
必ず「自分の手で」実際に計算式を書いていこう。そうすることによって、理解が格段に増します。
2⃣ 速さの最大値
\(x=0\)で弾性エネルギー\(\frac{k}{2} x^2=0 \)と最小になるとき、(✩)より運動エネルギー \(\frac{m}{2} v^2\)は最大で\(v\)最大となる。それを\(v_1\)とおくと、(✩)より
\(\displaystyle \frac{m}{2} {v_1}^2 +\frac{k}{2} 0^2 =\frac{m}{2} {v_0}^2 +\frac{k}{2} {x_0}^2\)
両辺を\(\displaystyle \frac{2}{m} \)倍して \(\displaystyle {v_1}^2 ={v_0}^2 +\frac{k}{m}{x_0}^2 \)
∴ \(\displaystyle v_1=\sqrt{{v_0}^2 +\frac{k}{m}{x_0}^2} \)
以上をまとめたのが図4。おもりは\(-A≦x≦A\)の範囲を(摩擦がなければ)何度も往復し続ける。これを単振動という。例えば\(v=0\)のとき右端\(x=A\)に達する理由は ―― 右向きに移動しながら\(v=0\)になるといったん停止するから、それ以上右へ行かず、しかもその瞬間ばねは伸びていて物体を引張っているからそこでUターンし、以後左向きに移動する。ということは\(v=0\)のときが右端\(x=A\)に達する瞬間というわけである。
単振動の詳しい内容は1-22-1以後の単元で扱うことにしよう。