1-45-2: ばねの両端 ー 重心から見た相対運動 ＃その2

1-45-1に引き続いて、ばね相互作用の具体的な計算をしましょう！　→　＜続き＞は1-45-3,1-45-4へ　

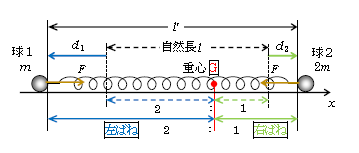
　振幅や周期などを求めるために、重心Gの左側の部分のばね（左ばねと呼ぶ）と右側の部分のばね（右ばね）に2分割して考えて（図１）、左ばね、右ばねのばね定数\(k_1,k_2\)を求めることにする [ この考え方の有用性はまもなく分かるので、なぜ分割？と手を止めたりせず、話に付いてくることが大切 ] 。1-45-1の通り重心から見ると、2球の変位は互いに逆向きで|変位|は質量の逆比\(m_2:m_1=2m:m=2:1\)だから、左ばねののび\(d_1\):右ばねののび\(d_2\)=2:1。いま、時刻\(t\)のばねの長さを\(l’\)とおけば、ばね全体ののびは\(l’-l\)だから、
　\(d_1=\frac{2}{2+1}(l’-l)=\frac{2}{3}(l’-l)\) ,　\(d_2=\frac{1}{2+1}(l’-l)=\frac{1}{3}(l’-l)\)
　弾性力\(F=k\)×(のび)から分かる通り、ばね定数\(k\)の定義は
　\(\displaystyle k=\frac{F}{のび}\)　　ゆえに、右ばねのばね定数\(\displaystyle k_2=\frac{F}{右ばねののびd_2}\)　　　　　　　　(1)
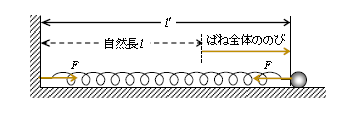
　ここで、\(F=k\)×(ばね全体ののび)\(=k(l’-l)\)であって、\(F=k\)×(右ばねののび)\(=k\frac{1}{3}(l’-l)\) ではないことに注意する。なぜなら ―― まず、図２のようにばねの左端が壁に固定されている場合、ばねが両端に等大の力\(F\)を加える際の\(F=k\)×(ばね全体ののび)\(=k(l’-l)\) であることに、異論はないだろう。ところで、弾性力はばねが生み出すもので、その「力の規則」(1-14-1ポイント欄)はばねの属性(ばねが全体としてどれだけ伸びたり縮んだりしたか)により決まる。ゆえに、ばねの両側の物体が運動しているのか(図１球１)静止しているのか(図２壁)にはよらず、\(F=k\)×(ばね全体ののび)になるというわけである。

　ということで、(1)より　\(\displaystyle k_2=\frac{k(l’-l)}{\frac{1}{3}(l’-l)}=3k\)　　　　　　　　　　　　　　　(2)
　\(k_2=3k \)の意味は、「右ばねは全体のばねに比べて\(\frac{1}{3}\)しか伸びていないのに、全体のばねと同じ大きさの弾性力\(F\)を生み出しているから、ばね定数が全体のばねよりも3倍だけ強いばねである」と捉えことができる。
　同様に、左ばねのばね定数\(\displaystyle k_1=\frac{F}{左ばねののびd_1}=\frac{k(l’-l)}{\frac{2}{3}(l’-l)}=\frac{3}{2}k \;\)　　　　 (3)
　では、以下1⃣2⃣3⃣と計算を進めていこう。1-45-1の図２を下に図３として再掲しておく。

1⃣ 振幅\(A_1,A_2\)
　1-18-1のエネルギー保存則\(\displaystyle \frac{m}{2} V^2 +\frac{k}{2} X^2=\)一定　を使うのが簡単だ。まずは右ばねだけに注目する（図３）。\(t=\frac{T}{4}\)は右ばねの単振動の左端にあたる点だから\(V_2=0\)(1-18-1)で、\(X_2=-A_2\)。また\(m_2=2m,k_2=3k\)（(2)より）にも注意して、エネルギー保存を\(t=\frac{T}{4}\)と\(t=0\)について立てると、
　\(\displaystyle \frac{2m}{2}0^2+ \frac{3k}{2}(-A_2)^2=\frac{2m}{2}\left(-\frac{v}{3}\right)^2+ \frac{3k}{2}0^2\)　　∴　\(\displaystyle {A_2}^2=\left(\frac{v}{3}\right)^2\frac{2m}{3k}\)　　
　∴　\(A_2=\)\(\displaystyle \frac{v}{3}\sqrt{\frac{2m}{3k}}\)　　[ 緑の下線は入試でよく聞かれる問題の答という意味 ]
　次に、1-45-1で述べた\(A_1:A_2=2:1\)を用いて　\(A_1=2A_2=\)\(\displaystyle \frac{2v}{3}\sqrt{\frac{2m}{3k}}\)
　[ \(A_1\)は、(3)の\(k_1=\frac{3}{2}k \)に注意して左ばねのエネルギー保存　
　　\(\displaystyle \frac{m}{2}0^2+ \frac{\frac{3}{2}k}{2}{A_1}^2=\frac{m}{2}\left(\frac{2v}{3}\right)^2+ \frac{\frac{3}{2}k}{2}0^2\)　を立てても求まる ]
　ばね全体の振幅\(A=A_1+A_2=2A_2+A_2=3A_2=\)\(\displaystyle v\sqrt{\frac{2m}{3k}}\)

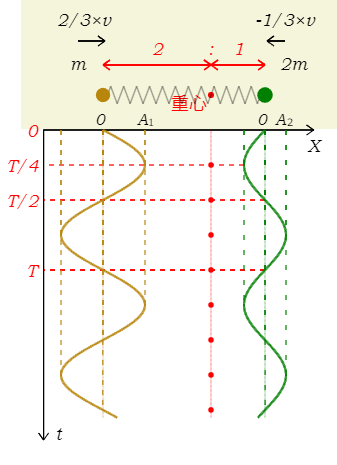
2⃣ ばねが初めて自然長に戻る\(t=\frac{T}{2}\)での\(V_1,V_2\)
　右ばねのエネルギー保存を\(t=\frac{T}{2}\)と\(t=0\)について立てると（図３）、
　\(\displaystyle \frac{2m}{2}{V_2}^2+ \frac{3k}{2}0^2=\frac{2m}{2}\left(-\frac{v}{3}\right)^2+ \frac{3k}{2}0^2\)　　∴　\(V_2=\)\(\displaystyle\frac{v}{3}\)　
　[ \(t=\frac{T}{2}\)と\(t=0\)の\(X_2\)はともに0だから、弾性エネルギーもともに0、したがって力学的エネルギー保存により運動エネルギーどうしが等しいので、\(|V_2|\)はともに等しい ]
　1-45-1の通り重心から見ると、2球の速度は互いに逆向きで|速度|は質量の逆比だから、
　\(V_1:V_2=(-2):1\)　　∴　\(V_1=-V_2=\)\(\displaystyle -\frac{2v}{3}\)
　なお、入試で\(t=\frac{T}{2}\)での床から見た速度\(v_1,v_2\)を問われたなら、重心から見た相対速度(重心が止まって見える観測者から見た速度)\(V_1,V_2\)に、1-45-1で求めた重心自体の速度\(v_G=\frac{v}{3}\)を足して
　\(\displaystyle v_2=V_2+v_G=\frac{v}{3}+\frac{v}{3}\)=\(\displaystyle \frac{2v}{3}\)
　\(\displaystyle v_1=V_1+v_G=-\frac{2v}{3}+\frac{v}{3}\)=\(\displaystyle -\frac{v}{3}\)　とする。
　ついでながら、\(t=\frac{T}{4}\)は左ばね・右ばねの単振動の端点で相対速度\(V_1=V_2=0\)だったから(1⃣)、床から見た速度は\(v_1=v_2=v_G\)。つまり、ばねがもっとも縮んでいる\(t=\frac{T}{4}\)では、重心から見て球1,2が静止しているがゆえに、床から見て球1,2,重心は全て同じ速度で動いている。もっとも伸びている\(t=\frac{3T}{4}\)も同様。

3⃣ 周期\(T\)
　周期公式(1-24-1)\(\displaystyle T=2\pi \sqrt{\frac{m}{k}}\)より、
　右ばねの\(\displaystyle T_2=2\pi \sqrt{\frac{m_2}{k_2}}=\)\(\displaystyle 2\pi \sqrt{\frac{2m}{3k}}\)
　ばねの左側が壁で固定されている質量\(2m\)の球単独の単振動(図２)では、周期\(\displaystyle T’=2\pi \sqrt{\frac{2m}{k}}\) 。\(T_2\)と\(T’\)を比べると、分母が\(T_2\)の方が\(T’\)よりも大きいから、\(T_2<T’\) 。この式の意味は、「右ばねは全体のばねに比べてばね定数が大きいから、ばねの引く[押す]力が大きく、すぐにつり合い点(自然長)に戻るので、周期が短い」と理解できる。このように、2球がともに動くばね相互作用は、一方の球だけが動く単振動に比べて周期が短いのが特徴である。
　同様に、左ばねの\(\displaystyle T_1=2\pi \sqrt{\frac{m_1}{k_1}}=2\pi \sqrt{\frac{m}{\frac{3k}{2}}}=\)\(\displaystyle 2\pi \sqrt{\frac{2m}{3k}}\)
　\(T_1=T_2\)となるのは、1-45-1で「2球が互いに逆向きに動きつつ、同じ周期で単振動する」と述べたことから当然である。