1-45-4: ばねの両端 ー 片方から見た相対運動 #その2
ばね相互作用の相対運動の締めくくりの単元です。
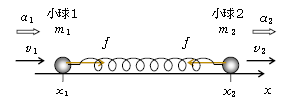
問題設定は1-44-1と同じで、図1に1-44-1の図1を再掲してある。
まずは発展的内容を1つ補足しておく。「床から見た球1,2の位置\(x_1,x_2\)を\(t\)の関数で表せ」と言われたら?具体的には、1-45-1のように (\(t=0\)での値に*を付けて)\(x^*_1=0\),\(x^*_2=l\), \(v^*_1=v>0\),\(v^*_2=0\)かつ\(m_1=m,m_2=2m\)の場合を扱う。このとき、ばねの長さ\(r\)は1-45-3(7)式の通り
\(\displaystyle r=-v\sqrt{\frac{2m}{3k}}\sin\sqrt{\frac{3k}{2m}}t+l\,\) (a)
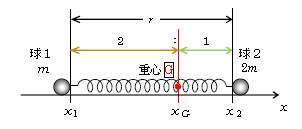
1-43-1の通り、重心Gは\(x_1,x_2\)を質量の逆比\(m_2:m_1=2m:m=2:1\)に内分する点だから、図2が書ける。ゆえに時刻\(t\)での
\(\displaystyle x_1=x_G-\frac{2}{2+1}r=x_G-\frac{2}{3}r\) (b)
\(\displaystyle x_2=x_G+\frac{1}{2+1}r=x_G+\frac{1}{3}r\) (c)
つまり、重心の項\(x_G\)と重心から見た相対位置の項\(-\frac{2}{3}r,+\frac{1}{3}r\)を組合せて考えればよい。
重心Gは1-44-1のように重心速度\(v_G=\frac{v}{3}=\)一定の等速度運動をするから、\(x_G=x^*_G+v_Gt\) 。ここで重心Gの初期位置\(x^*_G\)は、1-43-1の通り
\(\displaystyle x^*_G=\frac{m_1x^*_1+m_2x^*_2}{m_1+m_2}=\frac{m0+2ml}{m+2m}=\frac{2l}{3}\) ∴ \(\displaystyle x_G=\frac{2l}{3}+\frac{v}{3}t\)
この\(x_G\)の式と(a)の\(r\)を(b)(c)に代入したものが、求める\(x_1,x_2\)である。
では、1-45-3の球1から見た球2の相対運動の代わりに、球2から見た球1の相対運動を調べていくことにする。直観的には、多くの場合、前者の量の符号を逆にしたものが後者になるはず。だが、数式をきっちり扱う練習のつもりで図1に立ち戻ってしっかり行こう。運動方程式は1-44-1の通り
球1: \(m_1a_1=+f=+k(x_2-x_1-l)\) (1)
球2: \(m_2a_2=-f=-k(x_2-x_1-l)\) (2)
球2から見た相対運動を扱うには、(1)÷\(m_1-\)(2)÷\(m_2\)とする。
\(\displaystyle a_1-a_2=\left(\frac{1}{m_1}+\frac{1}{m_2}\right)k(x_2-x_1-l)\,\) (3)
ここで左辺は球2から見た球1の相対加速度である(「から見た」を引き算する公式(1-30-1))。1-22-1の通り加速度\(a=\frac{d}{dt}v=\frac{d}{dt}\frac{d}{dt}x=\frac{d^2}{dt^2}x\)だから、
(3)の左辺\(\displaystyle =\frac{d^2}{dt^2}x_1-\frac{d^2}{dt^2}x_2=\frac{d^2}{dt^2}(x_1-x_2)\)
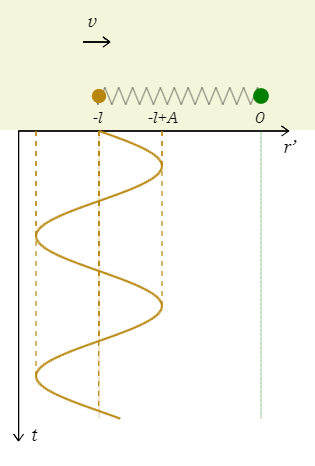
いま\(r’=x_1-x_2\)とおくと、\(r’\)は球2から見た球1の相対位置を表す。1-45-3の\(r=x_2-x_1\)(ばねの長さ)と\(r’\)は互いに逆符号だから、\(r’\)は時刻\(t\)でのばねの長さ\(×(-1)\)を表す。すると
(3)の左辺\(\displaystyle =\frac{d^2r’}{dt^2}\)
ゆえに(3)は \(\displaystyle \frac{d^2r’}{dt^2}=\left(\frac{1}{m_1}+\frac{1}{m_2}\right)k[-r’-l]\)
右辺の[ ]から\((-)\)をくくり出せば、
\(\displaystyle \frac{d^2r’}{dt^2}=-\left(\frac{1}{m_1}+\frac{1}{m_2}\right)k(r’-(-l))\) (4)
これは 変数\(r’\)の2階微分\(=-\)〇(\(r’-\)□) の形 で、変数\(r’\)の単振動の方程式(1-24-1)であると分かる。このように、右辺の(\(r’-\)□) の手前に\(-\)が付くような形に式変形をしていくことが重要である。
ここで、1-45-3の換算質量\(\mu\)を\(\displaystyle \frac{1}{\mu}=\frac{1}{m_1}+\frac{1}{m_2}\)として導入すれば、(4)は
\(\displaystyle \frac{d^2r’}{dt^2}=-\frac{k}{\mu}(r’-(-l))\)
これを単振動の方程式 \(\displaystyle \frac{d^2r’}{dt^2} =-\omega^2 (r’-r’_c) \) と比べて、
\(\displaystyle \omega=\sqrt{\frac{k}{\mu}}=\sqrt{\frac{k(m_1+m_2)}{m_1m_2}} \) , \(r’_c=-l\;\) (5) と読み取れる。
\(|r’_c|=l\)より、ばね相互作用は自然長\(l\)を中心値としてばねの長さ\(|r’|\)が長くなったり短くなったりすると分かる。また、\(\omega\) は1-45-3で求めた\(\omega\)と等しい。
ここで再び、1-45-2のように (\(t=0\)での値に*を付けて)\(x^*_1=0\),\(x^*_2=l\), \(v^*_1=v>0\),\(v^*_2=0\)かつ\(m_1=m,m_2=2m\)の場合を具体的に扱おう。このとき、
\(\displaystyle \omega=\sqrt{\frac{k(m+2m)}{m\cdot2m}}=\sqrt{\frac{3k}{2m}} \)
周期\(\displaystyle T=\frac{2\pi}{\omega}\)(1-23-1)\(\displaystyle =2\pi \sqrt{\frac{2m}{3k}}\) これは1-45-3の\(T\)と一致する。
いま、球2から見た球1の相対初期位置\(r’^*=x^*_1-x^*_2=-l\)、相対初速度\(u’^*=v^*_1-v^*_2=v\)
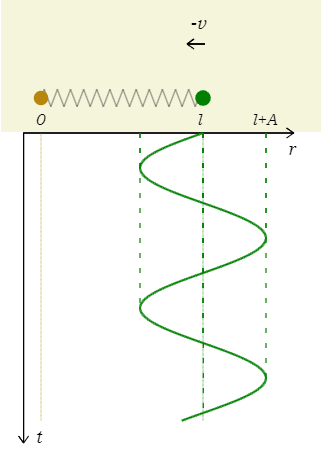
これはつり合い点(自然長の状態)で初速度\(v\)を与えるパターン(1-24-2)だから、図3のような+sin型のグラフになる(\(t\)軸を下向きに取った)。これを1-45-3の図2(再掲)と比べると、\(r’\)と\(r\)が互いに逆向きのグラフになっていることがよく分かる。振幅\(A\)を求めるには、公式「つり合い点にて\(v_{\text{max}} =A\omega\)」(1-24-2)より
\(u’^*=A{\omega}\) ∴ \(\displaystyle A=\frac{v}{\omega}=v\sqrt{\frac{2m}{3k}}\) これは1-45-3の\(A\)と一致する。\(r’\)を\(t\)の関数で表すと
\(\displaystyle r’=A\sin\omega t+r’_c=v\sqrt{\frac{2m}{3k}}\sin\sqrt{\frac{3k}{2m}}t-l\;\) (6) これは、この単元冒頭の式(a)の\(r\)の\((-1)\)倍である。