1-14-1: 弾性力
弾性力についてしっかり理解しておきましょう! → <例題>は1-14-2へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント 1-07-1と同様に「力の規則」を示す
| 何から | 向き | 大きさ | |
| 弾性力 | ばねから | ばねと平行 自然長に戻ろう とする向き | \(|F|=k|x| \)
\(k\): ばね定数[N/m] \(|x|\): のび・ちぢみ[m] |
図1、図2に示したのは、ばねの左端を壁に固定し、右端におもりを取り付けた図。ばねは引き伸ばされたり押し縮められると、自然長(ばねに何も手を加えていないときのオリジナルの長さ)に戻りたがる性質を持つので、自然長に戻ろうとする向きに弾性力を及ぼしてくる。伸びたばねは物体を引っ張り(図1 \(|F|\)が左向き)、縮んだばねは物体を押す(図2 \(|F|\)が右向き)。
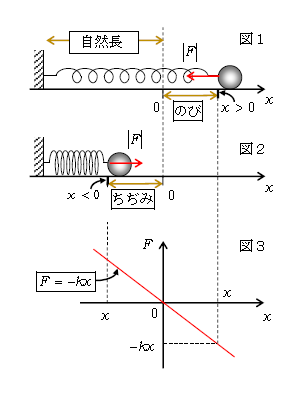
力の大きさ\(|F|\)は、のび\(|x|\)またはちぢみ\(|x|\)に比例し、比例定数を\(k\)(ばね定数あるいは弾性定数という)とすると\(|F|=k|x|\)である(フックの法則)。\(k\)の単位は\(\displaystyle k=\frac{|F|}{|x|}\)により[N/m]。
一方、\(F\)を符号付きで書けば、\(F=-kx\)。その理由は ――
のびのときは\(F\)は\(x\)軸の負の向き(図1)だから、\(F=-kx\)。
ちぢみのときは\(F\)は正の向き(図2)だが、実は\(F=+kx\)にはならない。というのも、ちぢみのときは\(x<0\)(図2)なので、\(F=+kx<0\)。これでは負の向きの力という意味になってしまう。むしろ\(-kx\)と書けば、\(F=-kx>0\)だから、正の向きの力という意味に合う。
縦軸に\(F\)、横軸に\(x\)を取った\(F\)-\(x\)グラフを書けば、図3のようになる。\(x\)軸上右向きに行ってのび\(|x|\)が増えるほど縦軸\(|F|\)が大きくなり、\(x\)軸上左向きに行ってちぢみ\(|x|\)が増えても縦軸\(|F|\)が大きくなる様子が見て取れる。縦軸\(|F|\)が大きくなるとは、図1、図2の力\(|F|\)の矢印が長くなるという意味。
\(F=-kx\)すなわち\(F\)は\(x\)に比例だから、当然\(F\)は一定ではない。すると運動方程式\(ma=F=-kx\)より\(\displaystyle a=-\frac{k}{m} x \)だから、\(a\)も\(x\)に比例し\(a\)も一定ではない。ということは、等加速度の公式は使えない。
ばねの問題では等加速度の公式を使わない、と心に刻んでおこう。
ではどうやって速度\(v\)や位置\(x\)を計算するのかと言えば、エネルギーの考え方を使うのが手っ取り早い。1-16、1-17でエネルギーを扱ってから、1-18-1で再びばねの問題に戻ろう。


