3-09-2: 電池

電池の正しいイメージを持つことが電気分野にとって重要です。　→　＜例題＞は3-09-3へ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　ここでは、前の単元の「極板間引力と静電エネルギーの関係」を再び題材にして、電池の重要事項を様々扱っていくことにする。
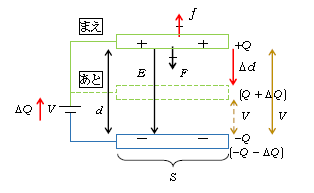
　図１の左下にある長短の横２本線が電池の回路記号で、長い方が電池の正極(乾電池の⊕側)、短い方が負極(⊝側)を表す。電池の左側に\(V\)とあるのは、正極と負極の間の電位差のことで、電圧、起電力ともいう。これらの言葉の微妙なニュアンスの違いは追々学んでいけばよく、当面は電位差＝電圧＝起電力と理解しておけばよい。単位は[V]。乾電池はふつう電圧1.5Vとして市販されている。図中には実線と点線があるが、まずは実線部分から。負極側の導線とそれに接続したコンデンサーの極板には、ひとつながりの導体は等電位という意味で青色を施してある。例えば青の電位を0Vとしよう。同様に正極側の導線とそれに接続した極板には緑色を施してある。電池は負極より正極の方が電位が\(V\)高い（また後で述べる）。ゆえに青を0Vとして、緑の電位は\(V\)。すると、コンデンサーの青の極板が0Vで緑の極板の電位が\(V\)だから、コンデンサーの電位「差」は\(V\)(黄色の実線）。そう、電池の電位差が\(V\)ならばコンデンサーの電位差も\(V\)。これを称して「電池の電圧がコンデンサーにかかる」という。　　　　　
　図１では、まえの状態(実線)の極板間隔\(d\)よりもあと(点線)の間隔の方が微小量\(\Delta d\)だけ短くなっている。あとの状態も電池の電圧がコンデンサーにかかるから、その電位差は\(V\)のまま(黄色の点線)。つまり、電池をつないだままだとコンデンサーの電圧は変わらない(一定のまま)。一方、3-08-1の容量\(\displaystyle C= \frac{\epsilon_0 S}{d} \)（\(S\):極板面積、\(\epsilon_0\):真空の誘電率）の分母の\(d\)があとの状態では\(d-\Delta d\)に減るから、\(C\)は増える。すると電荷\(Q=CV\)（3-08-1）も増えることになり、その変化量を\(\Delta Q\)とおけば、あとの状態の上極板(点線)の電荷は（\(Q+\Delta Q\)）、下極板の電荷は（\(-Q-\Delta Q\)）となる。このとき、まえからあとの過程で電池を電荷\(\Delta Q\)が通過する、その説明に移ろう。

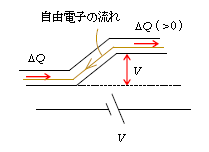
　まずは電流の間違ったイメージから。「下極板から\(\Delta Q\)が流れ出る。流れ出た\(\Delta Q\)は導線中を右回りに流れ、遠路はるばる上極板に到達する。上極板の電荷は\(Q\)から\(Q+\Delta Q\)になる。」これは全くの誤り。
　正しくは以下の通り。「導線のあらゆる所で(ほぼ)同時に\(\Delta Q\)が流れる。下極板の電荷が\(-Q\)から\(-Q-\Delta Q\)に変わると(ほぼ)同時に、上極板の電荷が\(Q\)から\(Q＋\Delta Q\)になる。」つまり、例えて言うなら電流とは、歯磨き粉のチューブの中を流れる歯磨き粉のようなもの。チューブのお尻を押すと(ほぼ)同時に出口から歯磨き粉が出る。お尻の歯磨き粉とは下極板から流れ出る\(\Delta Q\)の例え。出口から出る歯磨き粉とは上極板に流れ付く\(\Delta Q\)の例え。電流とは導線の各点各点で同時並行的に生じる流れだ。　　(☆)
以後このように電流をモデル化して回路を扱っていく。
　さて、電池と言えばボルタの電池、マンガン電池、リチウムイオン電池、太陽電池、電気二重層キャパシタ、…等々、その種類は多岐にわたる。これら全てを統一的に扱える電池のモデルが図２。電池は負極で電荷\(\Delta Q\)を吸い込むと(ほぼ)同時に正極で\(\Delta Q\)を吐き出す。ただし、\(\Delta Q\)の電位を\(V\)上昇させる。電位とは1Cあたりの持つ位置エネルギー[V=J/C]だから、電池は\(\Delta Q\)に対して仕事をしてその位置エネルギーを上げる役割を果たす。電池は電位をくみ上げるポンプのようなものだ。なお、負極で\(\Delta Q\)を吸い込むと(ほぼ)同時に正極でそれより少ない\(\Delta Q-10^{-6}\)Cを例えば吐き出すとすると、電池が\(10^{-6}\)Cの静電気を帯びることになるが、そのような状況は大学入試では決して扱われない。あくまでも\(\Delta Q\)を吸い込むと(ほぼ)同時に\(\Delta Q\)を吐き出す。
　ここで、前の単元のエネルギー保存則「系外から仕事を加えると、その分だけ系内のエネルギーが変化する」というエネルギーに関する宇宙の根本原理を、電荷\(\Delta Q\)という系に適用する（図２）。すると「電池が\(\Delta Q\)にした仕事の分、\(\Delta Q\)の位置エネルギーが増える」となる。結局、
　　電池のする仕事\(\Delta W=\)電池を通過する電荷×1Cあたりの位置エネルギー(電位)の増加\(=\Delta Q \cdot V\)
　　　　　[　　　J　　　＝　　　　C　　　　×　　　J/C　　　]

　電池の話はこれ位にして、冒頭で述べた「極板間引力と静電エネルギーの関係」が図１でどのようになっているかは、次の単元3-09-3の＜例題＞で考察することにする。