3-09-3: 極板間引力と静電エネルギー(電池付き)<例題>
この例題は難易度が少々高めなので、初めは解答を見ながらでもよいでしょう。前もって3-09-1,3-09-2を一読しておくことをおすすめします。
例題
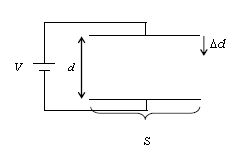
図のように、質量の無視できる極板どうしの間隔が\(d\)、極板の面積が\(S\)の平行平板コンデンサーに起電力\(V\)の電池をつなぎ、十分な時間経過させる。このときコンデンサーの蓄える電荷を\(Q\)とする。次に、極板どうしに働く引力\(F\)に逆らって正極板に外力\(f\)を加えつつ、正極板を図の下向きに微小な距離\(\Delta d\)移動させる。移動中電池はつないだままで、また極板どうしは平行な位置関係を保っている。電場は極板間のみに一様に生じているものとし、真空の誘電率を\(\epsilon_0\)とする。
(1) 電場を\(Q\)を用いて表せ。また、\(Q\)を用いずに表せ。以下では\(Q\)を答に用いてはいけない。
(2) 正極板を\(\Delta d\)移動させた後のコンデンサーの電荷を求めよ。
(3) 正極板を\(\Delta d\)移動させる間のコンデンサーの静電エネルギーの変化量\(\Delta U\)を、\(\Delta d\)に比例した形で表せ。必要ならば次の近似式を用いてよい:実数\(x\)の絶対値が1より十分小さいとき、\(\displaystyle \frac{1}{1-x}≒1+x \)
[ 注: 例えば\(\displaystyle \frac{1}{1-0.001}=\frac{1}{0.999}≒1+0.001 \)という意味の近似式 ]
(4) 電池のした仕事\(\Delta W\)を\(\Delta d\)に比例した形で表せ。
(5) \(f\)を\(\Delta U\)と\(W\)を用いて表せ。
(6) \(F\)を求めよ。
解答・解説
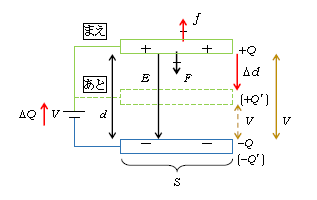
図1の通り極板間引力\(F\)が下向きなのでそれに逆らって加える外力\(f\)は上向き。外力\(f\)を上向きに加えつつ極板を下向きに移動するには、\(F\)よりも\(f\)を微小量だけ小さくしてやればいい。下向きの\(F\)が上向きの\(f\)よりごくわずかだけ勝って極板は下へ移動していく。
(1) 3-08-1より電場\(E=\) 答 \(\displaystyle \frac{Q}{\epsilon_0 S} \)
\(V=Ed\) より \(E=\) 答 \(\displaystyle \frac{V}{d} \)
(2) ∴ \(\displaystyle V=\frac{Q}{\epsilon_0 S} d=\frac{d}{\epsilon_0 S} Q \) ∴ \(\displaystyle Q=\frac{\epsilon_0 S}{d} V \) ①
3-09-2でやった通り、電池をつないだままだからコンデンサーの電圧\(V\)は一定である。\(\Delta d\)移動させた後の電荷\(Q’\)は、①の分母の\(d\)を\(d-\Delta d\)に置きかえることにより、
\(Q’=\) 答 \(\displaystyle \frac{\epsilon_0 S}{d-\Delta d} V \; \) ②
(3) 3-08-2より、静電エネルギー\(\displaystyle U=\frac{1}{2}QV \)の変化量は
\(\Delta U=\)あとの\(U’-\)まえの\(U=\)\(\displaystyle \frac{1}{2}Q’V-\frac{1}{2}QV=\frac{1}{2}(Q’-Q)V \) ③
②、①を③に代入して
\(\displaystyle \Delta U=\frac{1}{2} \left( \frac{\epsilon_0 S}{d-\Delta d}V – \frac{\epsilon_0 S}{d}V \right) V = \frac{\epsilon_0 S}{2} V^2 \left(\frac{1}{d-\Delta d}-\frac{1}{d} \right) \) ④
問題文中の近似式を用いると \(\displaystyle \frac{1}{d-\Delta d}=\frac{1}{d(1-\frac{\Delta d}{d})} \)
\(\displaystyle \)≒\(\displaystyle \frac{1}{d} \left( 1+\frac{\Delta d}{d} \right)=\frac{1}{d}+\frac{\Delta d}{d^2} \)
これを④に代入して \(\displaystyle \Delta U= \frac{\epsilon_0 S}{2} V^2 \left(\frac{1}{d}+\frac{\Delta d}{d^2}-\frac{1}{d} \right) \)
\(=\) 答 \(\displaystyle \frac{\epsilon_0 S}{2d^2} V^2 \Delta d \)
(4) 図1のようにコンデンサーの電荷が\(Q\)から\(Q’\)に変化するときは、3-09-2の通り電池を電荷\(\Delta Q=Q’-Q\)が通過しており、電池の仕事\(\Delta W=\Delta Q \cdot V=(Q’-Q)V \)。ところが③を用いると \(\Delta W=2\Delta U \)。
あとは(3)の答を代入して \(\Delta W=\) 答 \(\displaystyle \frac{\epsilon_0 S}{d^2} V^2 \Delta d \)
(5) 3-09-1のエネルギー保存「系外から仕事を加えると、その分だけ系内のエネルギーが変化する」を、コンデンサーという系に適用する。すると
「外力がした仕事と電池がした仕事\(\Delta W\)の分、静電エネルギーが\(\Delta U\)だけ変化する」⑤
となる。外力\(f\)は上向き、極板の移動は下向きで、力の向きと移動の向きが逆向きのときは仕事が負であることに注意すると、外力\(f\)のした仕事\(W=-f\Delta d \)。よって⑤より
\(-f\Delta d +\Delta W=\Delta U \) ∴ \(f=\) 答 \(\displaystyle \frac{\Delta W-\Delta U}{\Delta d} \)
<補足> 詳しい説明を付け足そう。いま\(Q\)が\(Q’\)に変化するから、\(\displaystyle E=\frac{Q}{\epsilon_0 S} \)も変化、\(\displaystyle F=Q\frac{1}{2}E\)(3-08-2)も変化、\(F\)とつり合う\(f\)も変化する。その変化量\(\Delta f\)を考慮して外力\(f\)のした仕事\(W=-(f+r\Delta f)\Delta d \)(rは例えば0.5のように選んだ適当な数)とでも書いてみる。すると\(W=-f\Delta d-r\Delta f \Delta d \)。ここで\(r\Delta f \Delta d \)は2次の微小量だから無視できる。よって\(W=-f\Delta d \)となる。
(6) つり合いより \(F=f\) だから、(5)の答に(4)、(3)の答を代入して
\(F=\) 答 \(\displaystyle \frac{\epsilon_0 S}{2d^2} V^2 \)
・ 3-08-1の容量\(\displaystyle C=\frac{\epsilon_0 S}{d} \)の式を用いると、\(F\)を次のように式変形できる。
\(\displaystyle F=\frac{\epsilon_0 S}{d} V\frac{1}{2}\frac{V}{d}=CV\frac{1}{2}\frac{Ed}{d}=Q\frac{1}{2}E\)
これは3-08-2で示した極板間引力\(F\)の式と一致している(!)。


