2-13-2: ドップラー効果 <例題>
例題を通じてドップラー効果の理解を深めましょう!
例題
水平な地面の上で、音をよく反射する平面状の壁を鉛直に取り付けた台車が静止している。いま台車が壁ととともに壁と垂直な方向へ一定の速さ\(u\)で地面上を動き出すと同時に、ある音源が台車と同じ向きに一定の速さで動き出した。音源は振動数\(f\)、波長\(\lambda \)の音波を四方に発している。この実験中の時間内に音源が壁に衝突することはないものとする。また、速さ\(u\)も音源の速さも音速より小さい。
問1 壁に届く音波の波長が\(\lambda ' \)であるとすると、音源の速さはいくらか。
問2 音源の速さ\(v\)、音速\(V\)とする。音源の進む方向と反対側に立っている観測者に、壁から反射して届く音波の振動数はいくらか。
問3 観測者は、壁から反射してくる音波と音源から直接届く音波が重なり合ってうなりを生じるのを聞いた。1秒間当たりのうなりの回数はいくらか。答は通分しない形で書いてもよい。
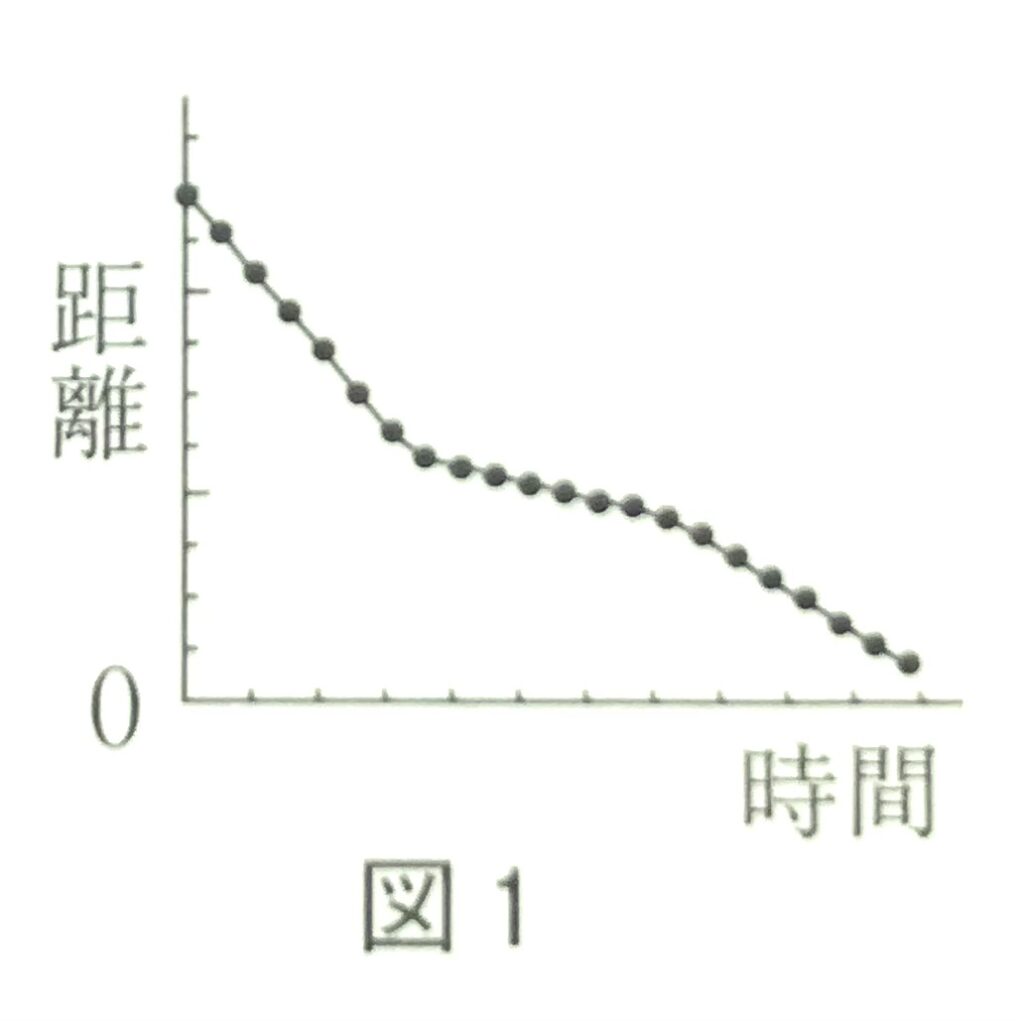
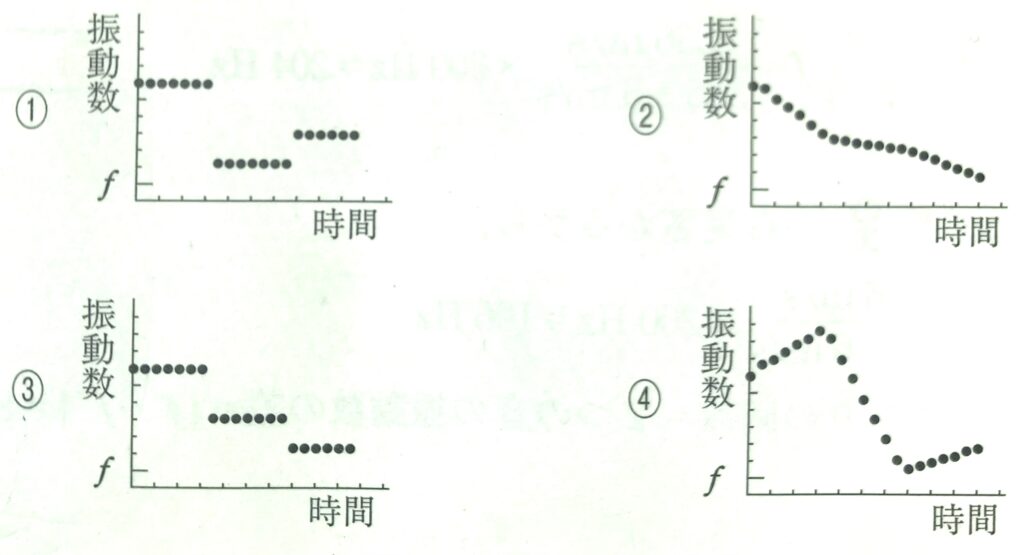
問4 次に台車を停止させる。その後音源が途中で速さを変えたため、台車の停止位置と音源との間の距離が図1のグラフのように変化した。このとき壁に届く音波の振動数はどのように変化したか。最も適当なものを、次の①~④のうちから一つ選べ。ただし、音波が音源から壁に届くまでの到達時間は無視できるものとする。
解答・解説
問題文の状況を表したのが図2。壁は音を反射する物体だから、このジャンルを反射体によるドップラー効果という。
問1 壁への入射波に関するドップラー(図2黄色の音波)。音源はAで、反射体上に観測者Bがいると想定すればよい。音の伝わる右向きを正として音源Aの速度\(v_s=v\)(これを求める)、観測者Bの速度\(v_o=u\) 。2-13-1の
波長公式\(\displaystyle \lambda '=\frac{V-v_s}{f}=\frac{V-v}{f} \)
ただし\(V\)は与えられていないので\(V=\lambda f \)と書きかえて
\(\displaystyle \lambda '=\frac{\lambda f-v}{f} \) ∴ \(\lambda ' f=\lambda f-v \) ∴ \(v=\) 答 \((\lambda -\lambda ')f \)
問2 引き続き、入射波について2-13-1の
振動数公式\(\displaystyle f’=\frac{V-v_o}{V-v_s} f=\frac{V-u}{V-v} f \: \) (1)
次に壁からの反射波のドップラー(図2の赤い音波)。観測者はD、反射体上に音源Cがあると想定すればよい。ここで重要なのは、反射すること自体で振動数は変化しないから、音源Cの振動数は入射波の\(f’\)に等しいということ(この理由を知りたい人は2-16-1ポイント(I)のすぐ下の段落を参照してほしい)。音の伝わる左向きを正として音源Cの速度\(v_s=-u\)、観測者Dの速度 \(v_o=0\) 。
振動数公式\(\displaystyle f’’=\frac{V-v_o}{V-v_s}\) \(f’\) \(\displaystyle =\frac{V}{V+u} f’ \) [ (1)を代入 ]
\(\displaystyle =\frac{V}{V+u}\frac{V-u}{V-v} f =\) 答 \(\displaystyle \frac{V(V-u)}{(V+u)(V-v)} f \) (2)
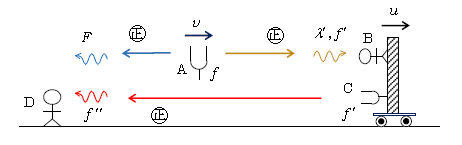
問3 図2の青い音波は音源Aから観測者Dへ、反射することなく直接届くから直接音という。音の伝わる左向きを正として音源Aの速度\(v_s=-v\)、観測者Dの速度\(v_o=0\) 。
振動数公式\(\displaystyle F=\frac{V-v_o}{V-v_s} f=\frac{V}{V+v} f \) (3)
問題文にあった通り、\(f’’\)と\(F\)とが重なってうなりが生じる。2-08-1より
1sあたりのうなりの回数=2つの音の振動数の差\(=|f’’-F|\) [ (2)(3)を代入 ]
\(\displaystyle =\left| \frac{V(V-u)}{(V+u)(V-v)} f – \frac{V}{V+v} f \, \right| \)
\(=\) 答 \(\displaystyle \left| \frac{V-u}{(V+u)(V-v)} – \frac{1}{V+v} \, \right| Vf \)
問4 図2の黄色の音波に関するドップラーを考えればよい。ただし、台車は停止しているから観測者Bの速度\(v_o=0\)、音の伝わる右向きを正として音源Aの速度\(v_s=v\) 。
振動数公式\(\displaystyle f’=\frac{V-v_0}{V-v_s} f=\frac{V}{V-v} f \)
ここで、\(v\)が大きいほど\(\displaystyle \frac{V}{V-v} \)の分母は小さく、\(\displaystyle \frac{V}{V-v} \)の値は大きいので、\(f’\)も大きい。
したがって、図1のグラフから\(v\)が大きい時間帯、小さい時間帯を読み取れば、それぞれが\(f’\)の大きい時間帯、小さい時間帯となる。 (*)
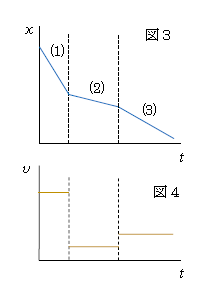
図1は1-01-1でやった\(x\)-\(t\)グラフに相当する(ここで\(x\)は台車の停止位置から左向きに測った音源までの距離)。それをあらためて図3に示す。\(x\)-\(t\)グラフの傾きは速度を表すことを思い出そう。図3のように時間帯に(1)~(3)の番号を付けると、傾きの絶対値(=速さ\(v\))の大きい方から順に(1)、(3)、(2)。ゆえに\(v\)-\(t\)グラフは図4のようになる。(例えば(2)なら(2)の1つの時間帯の中で見れば、\(x\)-\(t\)グラフの傾きは一定だから、(2)の中では\(v\)-\(t\)グラフは一定値を取る。)
(*)に述べたことから、求める\(f’\)-\(t\)グラフは図4と同じ概形のグラフを選んで 答 ①