3-09-1: 極板間引力と静電エネルギーの関係
コンデンサーの第4、第5公式をさっそく応用しましょう! → 関連事項は3-09-2へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 電池などを接続しないコンデンサー単体について
極板間引力に逆らって外力のする仕事=静電エネルギーの変化
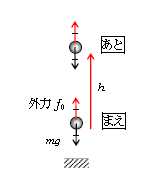
まずはイメージしやすい力学の話から。図1で小球に加わる重力\(mg\)につり合うように、上向きに例えば手で力を加えることを「重力に逆らって外力を加える」と表現する。外力\(f_0\)を\(mg\)よりも微小量だけ大きくしたり、\(mg\)に等しくしたりを繰り返すと、小球はほぼつり合いを保ちながら微小な速度できわめてゆっくりと上昇していく。すると、事実上速さ\(v=0\)だから運動エネルギー\(\frac{m}{2}v^2\)は無視してよい。このとき、図1のまえ状態からあと状態まで、外力\(f_0\)は仕事\(W_0=\)(力の移動方向成分)×(距離)\(=f_0h=mgh\)をしたと見なせる。これを「重力に逆らって外力のした仕事」\(W_0\)という。一方、まえからあとで重力による位置エネルギー\(U_0=mg\)×(高さ)は\(mgh\)だけ増えた。これを位置エネルギーの変化\(\Delta U_0=mgh\)であるという。したがって、次の関係式が成り立つことが分かる。
重力に逆らって外力のした仕事\(W_0\)=位置エネルギー変化\(\Delta U_0\)
この状況を次のように捉えることができる ―― 小球という「相手」に外から外力で仕事を加えた分だけ、「相手」のエネルギー(この場合は位置エネルギー)が変化した。 (1)
実はこれは、力学だけでなく、物理の全分野で成り立つ重要な関係だから、さらに説明を続けよう。
物理では「 系 」という用語をしばしば用いる。これはsystemの翻訳語で、英英辞典的には「複数の構成要素が関連し合って成す1つの全体」を指す言葉。例えばecosystem生態系は動物・植物様々な構成要素を含んでいる。物理では、2物体の成す「2体系」や、ばねとおもりからなる「力学系」などという使い方をする。
さて、(1)を一般化すると、「系外から仕事を加えると、その分だけ系内のエネルギーが変化する」 (2)
\(\displaystyle \)となる。これは力学・電磁気・熱力学など各分野の各事項ごとに個別に証明可能な場合がほとんどであるが、究極的にはエネルギーに関する宇宙の根本原理に位置づけられる。つまり、証明することなく、その正しさに信頼を寄せて安心して使ってよい。なお、(2)を「エネルギーと仕事の関係」と言ったり「エネルギー保存則」と言ったりする。(自然界のエネルギーは保存するという意味。つまり系外から仕事を加えた主体のエネルギーはその分だけ減り、一方その分だけ系内のエネルギーは増え、自然界のエネルギーの合計としては一定のままである。)
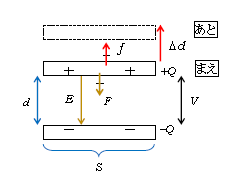
では本論に入ろう。図2に示したのは、極板間引力\(F\)に逆らって外力\(f\)を加え、極板間隔\(d\)を\(\Delta d\)広げる様子。極板の質量は無視している。ここで、電荷\(Q\)の値は変化しない(極板から\(Q\)が流れ出すことはないし、極板に新たに電荷が付着することを実験的に想定していないから)。3-08-1の通り、電場\(\displaystyle E= \frac{Q}{\epsilon_0 S}\)(\(S\):極板面積、\(\epsilon_0\):真空の誘電率)だから\(E\)も変化しない。ところが、3-08-1の電位差\(V=Ed\)の\(d\)が\(\Delta d\)変化しているから、\(V\)は変数だ。\(F\)の公式はまだ知らないつもりで、(2)の関係式をコンデンサーという系に適用することにより\(F\)を求めることにしよう(これは入試でよく出題される)。
(2)の左辺、系外から加えた仕事は外力のした仕事\(W=f\Delta d=F\Delta d\)。右辺、系内のエネルギー変化は静電エネルギー\(U\)の変化\(\Delta U\)。ゆえに(2)は
\(F\Delta d=\Delta U\) (3)
となるから、あとは\(\Delta U\)を計算すれば\(F\)が求まる。
3-08-2の通り\(\displaystyle U=\frac{1}{2} QV=\frac{1}{2} CV^2=\frac{Q^2}{2C} \)(\(C\):容量)であるが、上述のように\(V\)が変数なのでその変化量はぱっと見すぐには分からない。そこで\(V\)を含まない\(\displaystyle U=\frac{Q^2}{2C} \)を用いる。3-08-1の\(\displaystyle C= \frac{\epsilon_0 S}{d} \)を思い出すと、\(\displaystyle U=\frac{dQ^2}{2\epsilon_0 S} \)。すると、図2で
\(\Delta U=\)あとの\(U-\)まえの\(\displaystyle U=\frac{(d+\Delta d)Q^2}{2\epsilon_0 S}-\frac{dQ^2}{2\epsilon_0 S} =\frac{Q^2}{2\epsilon_0 S} \Delta d \)
よって(3)より \(\displaystyle F=\frac{Q^2}{2\epsilon_0 S} \)
ところが\(\displaystyle E= \frac{Q}{\epsilon_0 S}\)だから、 \(\displaystyle F=Q\frac{1}{2}E \)。これは3-08-2の結果に一致する。また、(2)を出発点として正しい\(F\)の式が得られたということは、出発点としての(2)が正しかったということのまさに裏付けになっている。


