3-03-3: 電場と電位＜例題２＞

3-03-2の例題１の続きです。問が難しすぎると感じたなら、まず解答・解説に目を通して考え方をしっかり理解しましょう！　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

例題　

　無限遠の点を電位の基準点とする。
問５　点Cに電気量\(-q\)（ただし\(q>0\)）を持つ質量\(m\)の荷電粒子を置く。粒子に働く静電気力に逆らって点Ｃから点Dまで移動させるために外力のする仕事を求めよ。   
問６　問５の荷電粒子を点Cに置き\(x\)軸の負の向きに速さ\(v_0\)を与えたところ、無限遠の点に遠ざかった。粒子に働く力は静電気力だけであるとして、点Ｃから無限遠の点まで粒子に加えられた仕事を求めよ。 
問７　問６で粒子が無限遠の点に遠ざかるための\(v_0\)の最小値を求めよ。

解答・解説

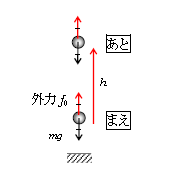
問５　まずはイメージしやすい力学の話から始める。図１で小球に加わる重力\(mg\)につり合うように、上向きに例えば手で力を加えることを「重力に逆らって外力を加える」と表現する。外力\(f_0\)を\(mg\)よりも微小量だけ大きくしたり、\(mg\)に等しくしたりを繰り返すと、小球はほぼつり合いを保ちながら微小な速度できわめてゆっくりと上昇していく。すると、事実上速さ\(v=0\)だから運動エネルギー\(\frac{m}{2}v^2\)は無視してよい。このとき、図１のまえ状態からあと状態まで、外力\(f_0\)は仕事\(W_0=\)(力の移動方向成分)×(距離)\(=f_0h=mgh\)をしたと見なせる。これを「重力に逆らって外力のした仕事」\(W_0\)という。一方、まえからあとで重力による位置エネルギー\(U_0=mg\)×(高さ)は\(mgh\)だけ増えた。これを位置エネルギーの変化\(\Delta U_0=mgh\)であるという。したがって、次の関係式が成り立つことが分かる。
　　重力に逆らって外力のした仕事\(W_0\)=位置エネルギー変化 あとーまえ \(\Delta U_0\:\)　(A)　
　この状況を次のように捉えることができる ―― 小球という「相手」に外から外力で仕事を加えた分だけ、「相手」のエネルギー(この場合は位置エネルギー)が変化した。
　一方、重力と外力は互いに逆向きだから、重力のした仕事は外力のした仕事の逆符号。ゆえに、
　　重力のした仕事=\(-\)(外力のした仕事)=\(-\)(位置エネルギー あとーまえ)
　　　　　　　　　=位置エネルギー まえーあと　　　　　　　　　　　　　　　(B)

　さて、問５で聞かれているのは「電気力に逆らって外力のする仕事」(電気力とほぼつり合いを保つ外力のする仕事)\(W\)である。ところで3-02-1の通り、電荷\(+Q\)(あるいは\(-Q\))のつくる電場は\(+Q\)(あるいは\(-Q\))からの距離の２乗に反比例して変わるから、一定ではない。すなわち(合成)電場\(\vec{E}\)も、負電荷\(-q\)に働く電気力\(\vec{F}=-q\vec{E}\)(3-02-1)も、それに逆らう外力も一定ではない。ゆえに、仕事\(W=\)(力の移動方向成分)×(距離)（1-16-1）と計算することはできない。このように力が一定ではない場合に仕事を計算するとき役立つ考え方が、(A)(B)を一般化した、以下の仕事と位置エネルギーの関係(1)(2)である。
　　保存力に逆らって外力のする仕事=位置エネルギー あとーまえ　　　　　　　(1)
　　保存力のする仕事＝位置エネルギー まえーあと\(\,\)　　　　　　　　　　　 　　 (2)　
　ここで保存力とは、簡単に言ってしまえば力学的エネルギーを保存させる力のことで、重力・弾性力・万有引力・電気力(クーロン力)の４つ（それ以外の摩擦力などは、力学的エネルギーを保存させない力で、非保存力という）。(2)の詳しい説明・証明は10-03-2にあるので、興味のある者は参考にしてほしい。　
　求めるのは「電気力に逆らって点Ｃ(まえ)から点D(あと)まで外力のする仕事」\(W\)であるから、(1)が使える。負電荷\(-q\)が点C,Dで持つ電気力による位置エネルギー\(U_C,U_D\)は、点C,Dの電位\(\phi_C,\phi_D\)を用いて\(U_C=-q\phi_C\), \(U_D=-q\phi_D\)と表せるから(3-03-1)、(1)より
　\(W=U_D-U_C=-q\phi_D-(-q\phi_C)=q(\phi_C-\phi_D)\;\:\,\)　　　　　　　　 (3)

　よって、(3)に3-03-2問２の\(\displaystyle \phi_C=\frac{2}{3}\frac{kQ}{l}\) 、問４の\(\displaystyle \phi_D=kQ\left(\frac{1}{d}-\frac{1}{ {\sqrt{4l^2+d^2}}}\right)\) を代入して
　\(W=\)　　　　答　 \(\displaystyle kQq\left(\frac{2}{3l}-\frac{1}{d}+\frac{1}{ {\sqrt{4l^2+d^2}}}\right)\)

問６　求めるのは「点C(まえ)から無限遠点(あと)まで電気力のする仕事」\(W’\)であるから、(2)より
　\(W’=-q\phi_C-(-q\phi_{\infty})\)　ここで\(\phi_{\infty}\)とは無限遠点の電位のことである。問題文中の「無限遠の点を電位の基準点とする」とは、「\(\phi_{\infty}=0\)とする」という意味（例えば重力による位置エネルギーの基準点とは、位置エネルギーを０と決める所という意味）。ゆえに
　\(W’=-q\phi_C\)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(4)
[　問題文で聞かれているのは、外力の仕事(1)なのか、電気力の仕事(2)なのか、注意深く読み取ろう　]
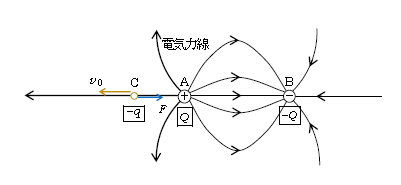
[　＜補足＞　図２に\(+Q\)と\(-Q\)のつくる電気力線の様子を図示してある（3-02-1図３の再掲）。点Cを通って左向きに真っ直ぐ力線が伸びているが、力線の向きは電場\(\vec{E}\)の向き。負電荷\(-q\)に働く電気力\(\vec{F}=-q\vec{E}\)(3-02-1)で\(\vec{F}\)と\(\vec{E}\)は逆符号。ということは、負電荷\(-q\)は力線(電場)の向きと逆向き(右向き)に力\(\vec{F}\)を受ける。初速\(v_0\)が左向きで、右向きに力を受けるから、負電荷\(-q\)は左へ行きながら減速するが、それでもなお\(-x\)方向の無限遠点に遠ざかった ―― そんな題意である。このように電気分野では、電気力線の様子をイメージしながら現象をつかむようにすることが大切だ。 ]

　(4)に3-03-2問２の\(\displaystyle \phi_C=\frac{2}{3}\frac{kQ}{l}\) を代入して　\(W’=\)　　　　答　 \(\displaystyle -\frac{2kQq}{3l}\)

問７　問６の＜補足＞で、電気力線の様子から負電荷\(-q\)は左へ行くほど減速すると述べた。その説明には電場(1Cあたりに働く力3-02-1)の考え方を用いた。
　一方、左へ行くほど減速することを、電位(1Cあたりの持つ位置エネルギー3-03-1)の考え方を用いて説明することもできる ―― 3-03-1の通り、電気力線の向きに電位は下がる。図２より、点Cを通って左向きに真っ直ぐ力線が伸びているので、左へ行けば行くほど、電位\(\phi\)は(単調)減少していく。位置エネルギー\(U=-q\phi\)(3-03-1)は\(\phi\)と逆符号なので、位置エネルギー\(U\)は増えていく。力学的エネルギー保存により運動エネルギーと位置エネルギーの和は一定だから、位置エネルギーが増えるというこは、運動エネルギー\(\frac{m}{2}v^2\)は減る、すなわち速さ\(v\)は減っていく。 
　このように電気力線の様子をイメージしつつ、力の考え方とエネルギーの考え方を併用することで、電気分野の理解は格段に深まり、また習得も早くなる。
　さて、求めるのは運動エネルギーが(単調)減少しつつも無限遠点に遠ざかる条件。これを求めるには以下のようにする。まず無限遠点での運動エネルギー\(\frac{m}{2}v_{\infty}^2\)が残っていると「仮定」して、力学的エネルギー保存を立てる。
　　　　まえ　　　　　　　　　あと    
　\(\displaystyle \frac{m}{2}v_0^2+(-q\phi_C)\;=\;\frac{m}{2}v_{\infty}^2+(-q\phi_{\infty})\) 
　　　　　　　　　　 \(\displaystyle =\;\frac{m}{2}v_{\infty}^2\)　　[ \(\phi_{\infty}=0\)を代入した ]
　右辺の \(\frac{m}{2}v_{\infty}^2<0\)ならば、2乗の量が負になるはずもないから矛盾。ゆえに背理法により「仮定」が間違っていたと分かり、 \(\frac{m}{2}v_{\infty}^2\)は残っていないということになる。一方、\(\frac{m}{2}v_{\infty}^2≧0\) なら、粒子は無限遠点で速さを持ちつつ運動(\(v_{\infty}>0\))またはちょうど静止(\(v_{\infty}=0\))するから、無限遠点に達していることになる。こうして、求める条件は右辺=\(\frac{m}{2}v_{\infty}^2\)≧0、すなわち
　左辺=\(\displaystyle \frac{m}{2}v_0^2+(-q\phi_C)≧0\)　　問２の\(\displaystyle \phi_C=\frac{2}{3}\frac{kQ}{l}\)を代入して　
　\(\displaystyle \frac{m}{2}v_0^2≧q\frac{2}{3}\frac{kQ}{l}\)　　　　∴　\(v_0≧\)　答　 \(\displaystyle 2\sqrt{\frac{kQq}{3ml}}\)