1-48-1: 万有引力の法則
これからの単元はしばらく万有引力の法則に関わる現象を取り扱っていきます! → 関連単元は1-48-2第1宇宙速度・第2宇宙速度、1-48-3静止衛星<例題>、1-49-1ケプラーの法則、1-49-2ケプラーの法則<例題>
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント ・ 万有引力の法則
| 何から働く | 向き | 大きさ | |
| 万有引力 | 質点どうしで働く | 引力 | 以下の通り |
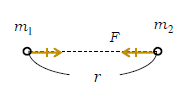
力の大きさ\(\displaystyle F=G\frac{m_1 m_2}{r^2} \) (1)
\(m_1, \, m_2\): 質量[\(\text{kg}\)] \(r\): 2質点間の距離[m]
\(G\): 万有引力定数=6×10\(^{-11}\)[N\(\cdot \)m\(^2\)/\(\text{kg}^2\)]
\(F\)は2質量の積\(m_1 m_2\)が大きいほど、
2質点の距離\(r\)が小さいほど、大きい
・ 万有引力による位置エネルギー
\(\displaystyle U=-G\frac{m_1 m_2}{r}\) (2)
・ 地表面での万有引力=重力
\(\displaystyle G\frac{Mm}{R^2}=mg\) ∴ \(GM=gR^2\)
万有引力の法則は、ニュートンが、自身の編み出したニュートンの運動の法則と、当時知られていたケプラーの法則などに着想を得て提唱した。その内容は上のポイントに示した通り。
この法則がなぜ成り立つのか、と聞かないでほしい。むしろ、我々の宇宙はそれが成り立つようにできているという仮説を置いて、それが実験事実を見事に説明するから、この法則は成り立つと認めているのである。それの成り立たないまた別の宇宙があるのかもしれないが、そんな宇宙があるかどうかの答は現在の物理学にはない。ともかく我々の宇宙においては、万有引力の法則を出発点の式として認めよう。この出発点の式という意味においてこの法則は、「宇宙の根本原理」である。つまり、万有引力の法則は覚えなければいけない。この段落で述べたことは、1-05-1の運動方程式についての説明と全く同様である。
さて、いきなり結論を言うと、万有引力による位置エネルギー\(U\)(ポイント(2)式)なる量が存在する。力学的エネルギー保存則が成り立つ場合には
運動エネルギー\(\frac{m}{2}v^2+\)位置エネルギー\(U=\)一定 となる。
位置エネルギー(2)式はとりあえず覚えよう。位置エネルギーに(ー)が付くこと、分母が\(r^2\)ではなく\(r\)になっていること(距離\(r\)の1乗に反比例)も含めてしっかり覚えておきたい。なお、10-03-3に(2)の導出を載せてあるので、興味のある人は参考にしてほしい。
クーロン力や電位にすでになじみのある人にとっては、以下の説明が参考になるだろう。万有引力(ポイント(1)式)のように距離\(r\)の2乗に反比例する力としては、他にクーロン力もある。クーロン力による位置エネルギー\(U\)を引力の場合に考えよう。負電荷\(-q_1\)が正電荷\(+q_2\)のつくる電位\(\phi\)の下で持つ位置エネルギー\(U\)は、3-03-1より
\(\displaystyle U=-q_1\phi=-q_1\cdot k\frac{q_2}{r}=-k\frac{q_1q_2}{r}\)
そう、距離\(r\)の2乗に反比例する力が引力の場合、ちょうど(2)のように位置エネルギーに(ー)が付き、距離\(r\)の1乗に反比例の形になっている。
では、さっそく万有引力の法則の関わる現象の例を2つ見ていくことにしよう。
1⃣ 地表面での万有引力(図1)
地球を密度が一様な半径\(R\)の球体(質量\(m_1=M\))と捉え、地球からの万有引力を受ける物体も密度が一様な球体(質量\(m_2=m\))と見なそう。このように質点(その質量は考えるが大きさを無視する物体)ではなく、大きさのある密度が一様な球体どうしの間に働く万有引力に関しては、各々の球体の中心どうしの距離を\(r\)とすればポイント(1)式が成り立つことを、大学レベルで証明できる。高校物理では球体の中心間距離を\(r\)とすることを、証明抜きで知識として使ってよい。また、万有引力の分野では、特に断りがなくても密度が一様な球体どうしの万有引力を扱って出題している。
さて、\(m_2=m\)の物体を地表面に置き、その大きさを地球に比べて無視すれば、\(r=R\)となる。このとき物体に働く力は地球から働く万有引力\(F\)だけではない。地球は自転運動をしているので、遠心力\(f\)(回転系での慣性力)も入れなくてはいけない。遠心力は1-37-1の通り、回転軸(自転軸)と垂直な方向・軸から遠ざかる向きに、大きさ\(f=mr’\omega^2\)(\(r’\):物体と回転軸との距離、 \(\omega\):自転の角速度) である。
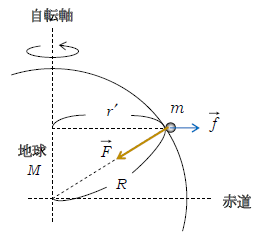
この\(\vec{F}\)と\(\vec{f}\)のベクトル和が実はふだん我々が重力(ベクトル)と呼んでいるものの正体である。が、実際に数値計算してみると、\(f\)は\(F\)に比べて無視できるほど小さいことが分かる。参考までに、例えば赤道面上での遠心力\(f=mR\omega^2<0.004F\)(\(F\)の数式はこの後すぐの(3)式にある)と求まったりする。ゆえに、通常\(f\)は無視して\(F\) ―― 地表面での万有引力が重力\(mg\)であると見なす。ポイント(1)の\(F\) の公式を用いて
\(F=\)\(\displaystyle G\frac{Mm}{R^2}=mg\) ∴ \(GM=gR^2\) (3)
さて、歴史的には、ニュートンの時代(18世紀)に重力加速度\(g\)≒9.8m/s\(^2\)、地球の半径\(R\)≒6400kmであることは知られていたが、地球の質量\(M\)の値は分かっていなかったし、したがって(3)より万有引力定数\(G\)の値も未知だった。ゆえにニュートンは、(3)を用いて\(GM\)を消去することによりいろいろな計算を押し進めた。万有引力分野の出題では(3)の書きかえをしばしば用いることになる。重要な式なのでしっかり押さえておこう。
2⃣ 地表から高度1km程度までの万有引力(図2)
1⃣と同様の文字\(R,M,m\)に加えて、地表面からの高度\(h\)として、物体に働く万有引力の大きさ\(F\)は
\(\displaystyle F=G\frac{Mm}{(R+h)^2}\) (4)
ところで、スカイツリーの高さが634m、富士山の高さが3776mであることを考えると、人間の日常生活の範囲は高度\(h\)=1km程度までとしてよいだろう。地球の半径\(R\)≒6400kmだから、\(h\)は\(R\)に比べて無視できる。すると(4)は
\(\displaystyle F=G\frac{Mm}{R^2}\) これは(3)より\(mg\)に等しい。
つまり、\(h\)=1km程度までなら、万有引力\(F\)は(4)のように\(h\)とともに変わったりせず、むしろ\(F=mg\)という一定値と見なせる。このような場合なら、放物運動に対して鉛直下向きの重力加速度\(g\)の考え方を当てはめていいし、重力による位置エネルギー\(mgh\)を用いて力学的エネルギー保存則を立ててよい。
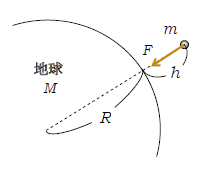
一方、たとえば\(h=2R\)≒12800kmや\(h=0.5R\)の宇宙規模の話になると、万有引力\(F\)は一定値と見なせない。宇宙規模の話では重力加速度\(g\)の等加速度運動の考え方は使えず、また、\(mgh\)ではなく万有引力による位置エネルギー\(U\)(ポイント(2)式)で力学的エネルギー保存則を立てなくてはいけない。
→ 関連単元は1-48-2第1宇宙速度・第2宇宙速度、1-48-3静止衛星<例題>、1-49-1ケプラーの法則、1-49-2ケプラーの法則<例題>


