1-37-1: 遠心力
遠心力は慣性力の一種です。しっかり押さえましょう!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 遠心力:回転座標系で運動方程式を成り立たせるために必要となる慣性力
向き:回転軸と垂直な方向、軸から遠ざかる向き
大きさ:\(mR\omega^2\)(\(R\):物体と回転軸との距離、
\(\omega\):静止座標系に対する回転座標系の角速度)
1-35-1で述べた通り、静止座標系から見るとは静止している観測者からものを見るという意味だった。この単元で回転座標系から見ると言うとき、それは回転軸上の観測者が回転しながらものを見るという意味。1-35-1と同様に、静止座標系・回転座標系をそれぞれ静止系・回転系と略す。
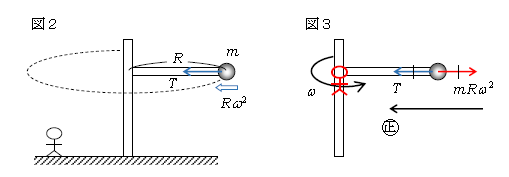
遠心力の説明の題材として図1を選ぼう。鉛直方向の棒を回転軸とし、水平方向の棒に取り付けた小球(以後球と呼ぶ)を、外力(例えば手の力)を加えながら一定の角速度\(\omega\)で水平面内を回転させる。これを静止系(床上に静止している観測者)から見たのが図2。棒からの張力\(T\)を受けて小球に向心加速度\(R\omega^2\)が生じている。円運動の方程式は
\(mR\omega^2=T\) (1)
ここで、図3のように回転系から球を眺めよう。つまり、回転軸上で球と同じ高さの目線を保ちながら角速度\(\omega\)で回転する観測者(人)を想定する。球が時間\(\Delta t\)の間に\(\omega\Delta t \)回ると、人の目線も等しく\(\omega\Delta t \)回るということは、人から見て球は同じ位置にとどまり続けて見えるということ。ゆえにつり合いの式が成り立つ。ただし、単純に\(0=T\) では静止系から見た運動方程式(1)、すなわち正しい方程式と食い違ってしまう。そこで図3のように赤い矢印\(mR\omega^2\)を見かけの力(慣性力)として書き足して、つり合いの式を書けば
\(0=T-mR\omega^2\) (2)
(2)は(1)と同値だから正しい方程式になっている。この\(mR\omega^2\)を遠心力と言い、ポイントにある通り、回転系における慣性力の一種である。遠心力の効果は、例えば遊園地のコーヒーカップ(乗り物)で自分の背中がカップの壁に押し付けられることから実感できる。そう、カップの回転軸から遠ざかる向きに我々は遠心力を受けて、背中が壁に圧迫される。
ここで、物理用語をしっかり整理しておきたい。(2)の右辺の\(mR\omega^2\)は遠心力であるが、(1)の左辺の\(mR\omega^2\)は遠心力ではない、と言うとドキッとする人もいるのではないか。それをしっかり押さえよう。運動方程式は因果法則「力という原因によって、結果的に加速度が生じる」だった。であるなら、回転系の方程式(2)の右辺は、遠心「力」\(mR\omega^2\)という原因と張「力」\(T\)という原因がプラスマイナス打ち消し合って、結果的に加速度を生じずつり合っているという意味になる。一方、静止系ではそもそも遠心力(慣性力の一種)のような見かけの力は存在しない。その方程式(1)の右辺は張「力」\(T\)という原因で、それによって結果的に向心加速度\(R\omega^2\)が生じるから床から見て球は円運動するという意味である。つまり静止系の(1)の左辺は、遠心「力」という原因でも何でもなく、あくまでも質量\(m\)×向心加速度(結果)\(R\omega^2\)に過ぎない。
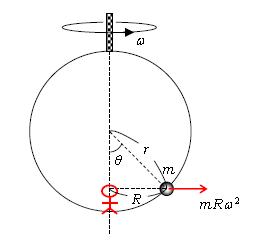
最後に図4のような場合の注意点を1つ。小球が半径\(r\)の円リングに通されて、その円リングが鉛直軸の周りに角速度\(\omega\)で回転するような場合。今までの説明から分かる通り、回転軸の観測者からの距離\(R\)(\(=r\sin\theta\))を用いて、遠心力は回転軸と垂直な方向(水平方向)に\(mR\omega^2\)となる(言い換えると、回転軸に物体から垂線を下した位置に観測者を想定する)。うっかり半径\(r\)に目が行き遠心力\(mr\omega^2\)としたり、あるいは半径\(r\)の延長線上に遠心力の矢印を書いたりしないこと。