1-22-1: 単振動の方程式

いよいよ、単振動の位置\(x\) と時間\(t\) の関係式\(x=A\sin(\omega t+\phi)+x_c \)に入っていきます！　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　この単元を学ぶ人は、前もって1-14-1: 弾性力 という単元に目を通しておくことをお勧めする。
　図１のように、天井から質量の無視できるばね定数\(k\)、自然長\(l\)のばねを吊るし、その先端に質量\(m\)の小球を取り付けてある。小球は鉛直方向のみを運動するものとし、重力加速度を\(g\)とする。左図はばねが伸びた状態、右図は縮んだ状態で、いずれも運動中の任意の瞬間を想定している。弾性力(黄色)の向きは自然長(\(x=l\)の位置)に戻ろうとする向きだから、左図では上向き、右図では下向き。弾性力の大きさは\(k\)×のび・ちぢみで、のび・ちぢみとは自然長からのずれ\(|x-l|\)。したがって、のびは\(x-l \)、ちぢみは\(l-x \)である。

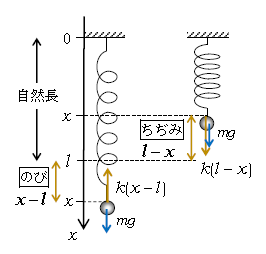
　運動方程式は、下向きを正として
　　のびの場合　　\(ma=-k(x-l)+mg \)　　　　　　　(1)
　　ちぢみの場合　\(ma=+k(l-x)+mg=-k(x-l)+mg\)
となるから、両者ともに同形である。のび\(x-l \)に対してちぢみ\(l-x \)は逆符号になるが、力の向きものびとちぢみで逆符号だから、結局 \(ma=-k(x-l) \cdots \) と同形になる。ということは、弾性力がらみの運動方程式は、のび・ちぢみの両方を図に書く必要はなく、一方だけ調べればよいということが言える。

　さて、つり合いの位置を\(x=x_c \)とおくと、(1)より \(0=-k(x_c-l)+mg \)
　　\(\displaystyle ∴　x_c=l+\frac{mg}{k} \)
　すると(1)は　\(\displaystyle ma=-k(x-l-\frac{mg}{k})=-k[x-(l+\frac{mg}{k})]　\)
　　　　　　　　　 \(=-k(x-x_c)\)　　と変形できるから、　
　　\(\displaystyle a=-\frac{k}{m} (x-x_c) \) 　　
　ここで \(\displaystyle \omega=\sqrt{\frac{k}{m}} \) とおくと後々便利で　
　　\(a=-\omega^2 (x-x_c) \)　　　　　　　　　　　　　　　　　(2)
　これが成り立つときは、1-23-1で見る通り必ず \(x=A\sin(\omega t+\phi)+x_c \) なる単振動の有名な公式が成り立ち、(2)を単振動の方程式という。これは単振動の定義式である。つまり、単振動（1-18-1で扱った往復運動）は、運動方程式を立てて\(a\)を求めれば、必ず
　　\(a=-\)〇(\(x-\)□) の形　になる。
　ということで、次の単元1-23-1でさっそく \(x=A\sin(\omega t+\phi)+x_c \) を導こう。

　なお、1-01-1、1-02-1でやった通り、速度\(\displaystyle v=\frac{dx}{dt} \)、加速度\(\displaystyle a=\frac{dv}{dt} \)だから、
　 \(\displaystyle a=\frac{d}{dt}v=\frac{d}{dt}\frac{d}{dt}x=\frac{d^2}{dt^2}x= \frac{d^2x}{dt^2}\)
　\(\displaystyle\)つまり(2)式は　\(\displaystyle \frac{d^2x}{dt^2} =-\omega^2 (x-x_c) \)
　これは、変数\(x\)の2階微分\(=-\)〇(\(x-\)□) の形　と読める。この形で覚えておくと応用が効いて便利だ。たとえば電気回路分野に入ったときの電荷\(Q\)が　変数\(Q\)の2階微分\(=-\)〇(\(Q-\)□) の形　になれば単振動の考え方が応用できる、などである。