1-01-1: 準備
まずはウォーミングアップから。基本事項をしっかり押さえましょう!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ \(x\)-\(t\)グラフの接線の傾きは速度に等しい
・ 速度の向きは運動の向きと等しい
速度の大きさを速さという
まずは、直線に沿って動く物体の運動「直線運動」を考えよう(図1)。このために、物体の運動方向に沿って\(x\)軸を取り、\(x\)座標で物体の位置を表す。例えば\(x=-\)3mというように。単位m、m/sなどは数値の後に\(-\)3m、5m/sと表記し、文字\(x\)、\(v\)の後にくる場合は[ ]を付けて\(x\)[m]、\(v\)[m/s]のように書くことが多い。

ある位置\(x\)と、時間がたったあとの位置\(x’\)があるとき(図2)、あとの位置\(x’\)からそれよりまえの位置\(x\)を引いた差\(x’-x\)を、位置\(x\)の変化量という。引く順番はあと-まえ、変化量=あと-まえ だ。
変化量は記号\(\Delta \)(デルタ)で表す。「\(\Delta x\)」と書けば、「\(x\)の変化量」のこと。\( \Delta x=x’-x \)を特に変位という。負の変位と言えば\(\Delta x=x’-x<0\)だから\(x'<x\)、つまり物体が\(x\)軸の負の向き(左向き)に動くという意味になる(図2)。例えば\(\Delta x=-5\)mのように、変位\(\Delta x\)は符号(\(+,-\))を持つ量だ。向きを持つと言ってもよい(\(\Delta x=-5\)mだったら変位は負の向きという)。
さて、図3は縦軸が\(x\)軸、横軸が\(t\)軸で、\(t\)は時刻を表す。横軸の右へ行くと時刻が\(t=\)1s、2s、… と経っていくという意味。青いグラフは\(x\)-\(t\)グラフと呼ばれる。時刻の変化\(\Delta t=t’-t \)を時間という(図3横軸に示してある)。変位\(\Delta x \)[m](縦軸に示してある)を時間\(\Delta t \)[s]で割ったもの\(\displaystyle \frac{\Delta x}{\Delta t} \)[m/s] を平均速度という。\(\Delta x ÷ \Delta t \)は点線の直角三角形のタテ÷ヨコだから、斜辺の傾きに等しい。
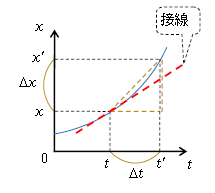
ところで物理では、\(\Delta t \)というある時間幅の中ではなく、時刻\(t\)なら\(t\)のまさにその瞬間の運動の様子を調べたいということがしばしば起こる。\(t\)の様子を正確に知るためには、\(\Delta t \)を限りなく小さく取って(図3横軸上の時刻\(t’\)を\(t\)に限りなく近付けて)\(t\)付近を限りなく細かく瞬間的に捉えればよい。\(\Delta t \)を限りなく小さく取ると、点線の直角三角形がどんどん小さくなり、その斜辺の傾き\(\Delta x\div\Delta t\)は接線の傾き(図3赤)に限りなく近付く。これを瞬間速度あるいは単に速度\(v\)という。
速度\(\displaystyle v=\frac{\Delta x}{\Delta t} \) (ただし\(\Delta t → 0\)) (1)
速度\(v\)は\(x\)-\(t\)グラフの接線の傾きに等しい。
参考 (1)式は \(\displaystyle v=\lim_{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t} \) とも書ける。
ここで\( \displaystyle \lim_{\Delta t \rightarrow 0} \bigcirc \)は数学の記号で、\( \bigcirc \)を計算するときに\( \Delta t \)を極限まで限りなく小さく取りなさい(つまり無限小にしなさい)という意味。limはlimit(極限)の略。
数学で微分を習った人はもう気付いていると思うが、(1)(接線の傾き)は数学の微分係数に他ならず、 \(\displaystyle v=\frac{dx}{dt} \) とも書ける。
変位\(\Delta x\)は符号・向きを持つから、(1)式より速度\(v\)も符号・向きを持つ。(1)より速度\(v\)と変位\(\Delta x \)の符号は等しいから、速度の向きは物体の変位の向き、すなわち運動の向きに等しい。一方、速さと言えば\(|v|\)のことで、絶対値だから符号を持たない。例えば正の向きの速度\(v=\)+2m/sも負の向きの速度\(v=\)-2m/sも、速さ\(|v|\)としては2m/sとなり、速さが右向きというような表現はない。


