1-15-1: 放物運動

いよいよ曲線運動に入っていきます。ここでは放物運動、1-19-1では円運動を扱います。　→　＜続き＞は1-15-2、1-15-3へ　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　この単元を学ぶ人は、必要ならば1-04-1: 落体の運動 に目を通しておくとよい。また、本参考書ではこの単元までベクトル記号をほとんど使ってこなかったが、これ以降は用いていく。
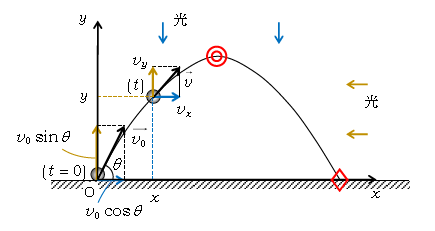
　物体が運動するにつれてその軌道がカーブを描く運動を「曲線運動」という。その代表例が小球を空中に投げたときの放物運動だ（図１）。「小」球と表現したなら、通常、球の大きさは無視するという意味になる（が、これ以後はくどくなるので単に球と記す）。球のそばに括弧付きで(\(t=0\))、(\(t\))と書いてあり、(\(t=0\))の方が初期条件の描図。つまり初速度が\(\vec{v_0}\)（水平方向となす角\(\theta\)）、初期位置が地面上の原点O。(\(t\))の方は時間\(t\)後の速度\(\vec{v}\)、位置座標 (\(x,y\)) 。
　ここで座標軸\(x,y\)を用いて運動を調べるとは、以下のような意味である。\(x\)軸上にスクリーンがあると想定し、光を\(x\)軸スクリーンに垂直に真上から当てると、球が動くとともに球の影も右へと動いていく。この影の動きは球の\(x\)座標の動きで、\(x\)軸上の直線運動。これを運動の\(x\)成分という。同様に光を\(y\)軸スクリーンに垂直に右から当てたときの影の動き、つまり\(y\)座標の\(y\)軸上の直線運動を運動の\(y\)成分という。運動の\(x,y\)成分、すなわち\(x\)軸、\(y\)軸上の２つの直線運動の組合せで曲線運動を調べようというわけである。2つの座標軸で記述できる曲線運動は2次元運動という。（一方、\(x\)軸だけで記述できる直線運動は1次元運動という。）
　速度\(\vec{v}\)とは1sあたりの変位[m/s]だから、図１で軌道の接線方向(変位していく方向)に\(\vec{v}\)と書いてある。ゆえに速度ベクトル\(\vec{v}\)の\(x\)成分\(v_x\)が意味するのは、球が\(\vec{v}\)の向きに\(　\vec{v}\Delta t \)変位すると、その影が\(x\)方向に\(v_x \Delta t \)変位するということ。つまり、\(v_x\)とは「\(x\)方向に沿う速度」とも言える。\(y\)成分\(v_y\)も同様。初速度\(\vec{v_0}\)の\(x,y\)成分は三角比により、それぞれ\(v_0\cos\theta,v_0\sin\theta\)（図１）。（なお、\(v_0=|\vec{v_0}|\)のことで、すなわち\(v_0\)は速さである。）
　赤い◎の印（図１）は球の「最高点」、◇の印は「落下点」で、よく出題される重要な箇所だ（1-15-2で扱う）。

　さて、1-08-1: 力学攻略の基本　の流れに従って行こう。
　まず軸と力（図２）　鉛直下向きに重力\(mg\)と書いた（球の質量を\(m\)、重力加速度を\(g\)とし、空気抵抗力は無視する）。加速度もあらかじめ図示しておいたが、加速度は正の向きに\(a_x,a_y\)と図示する、おくのが鉄則。仮に加速度\(a_x\)が(-8)のように負の値で求まったならば、負の向きに加速度が生じていると後で解釈すればよい。決して「右向きに\(a_x\)で加速中」という意味の図ではないので、念のため。
　次に \(m\vec{a}=\vec{F}\)　　[ ベクトル形で書いた。必要なら1-05-1を参照のこと ]
　ベクトルを成分表示すると　\(m(a_x \, , \,a_y)=(F_x \, , \,F_y) \)　　
　∴　 \(ma_x=F_x\) 、\(ma_y=F_y\)　　つまり、2次元運動では運動方程式は\(x\)成分、\(y\)成分2つ分ある。
　\(x\)成分: \(ma_x=F_x　=0 \)　　[ \(mg\)は\(-y\)方向に向いていて（図２）、
　　　　　　　　　　　　　　　　 \(x\)成分を持たないから\(F_x=0\) ]
　\(y\)成分: \(ma_y=F_y　=-mg \)　　[ \(mg\)は\(-y\)方向に向いているから\(F_y<0\) ]
　　∴　\(a_x=0\) 、\(a_y=-g\)
　\(a_x=0\)ということは、水平方向(運動の\(x\)成分)は加速しない、等速であるという意味。つまり、\(x\)座標は初速度の\(x\)成分\(v_0\cos\theta \)のまま等速直線運動していく。
　\(a_y=-g\)ということは、\(y\)軸が上向き正なので、鉛直方向(運動の\(y\)成分)は鉛直下向きの重力加速度\(g\)による等加速度直線運動であるという意味。これは1-04-1ですでに述べたことで、この単元でついにその証明をしたというわけである。

　なお、運動方程式を立てるときには力は必ず図示するとして、加速度は\(a_x,a_y\)のように図示しないまま、\(ma_x=\cdots \:、 \: ma_y=\cdots\)と立てるのも一法である。

　入試でよく扱われる計算例は、次の1-15-2で扱う。