1-15-2: 放物運動（続き）

放物運動の頻出の計算例をしっかりマスターしましょう！　→　1-15-3へ続く　　　　　　　　　　　　　　　　　　　　　　　　

　1-15-1の図を図１として再掲した。これを題材に、入試でよく扱われる以下の量を求めていこう。なお、速度の\(x\)成分は1-15-1の通り\(v_0\cos\theta\)のまま一定だから扱わない。また、\(a_x=0\)、\(a_y=-g\)である。
1⃣　最高点（図１の◎印）での時刻\(t_1\)、\(v_y\) 、\(x=l\)、\(y=h\)
　最高点では、1-04-1の通り\(v_y=0\) 。つまり、上昇速度\(v_y=0\)になると、まさにそれ以上上昇しなくなり、最高点に達する。
　すると等加速度の公式\(v=v_0+at\) の\(y\)成分バージョン\(v_y=v_{0y}+a_y t\) により、
　　\(\displaystyle \)\(v_y=0=v_0\sin\theta-gt_1 \)　　∴　\(t_1=\) \(\displaystyle \frac{v_0}{g} \sin\theta \)
　　[ 緑の下線は、入試問題でよく聞かれる問題の答という意味 ]
　等加速度の公式\(x=x_0+v_0 t+\frac{1}{2}at^2 \)の\(x\)成分バージョン\(x=x_0+v_{0x} t+\frac{1}{2}a_x t^2 \)より、
　　\(\displaystyle \)\(\displaystyle x=l=0+v_0\cos\theta \cdot t_1+0=v_0\cos\theta \cdot \frac{v_0}{g} \sin\theta =\)\(\displaystyle \frac{v_0^2}{g} \sin\theta\cos\theta \)
　\(y\)成分バージョン\(y=y_0+v_{0y} t+\frac{1}{2}a_y t^2 \)より、
　　\(\displaystyle y=h=0+v_0\sin\theta \cdot t_1-\frac{1}{2}gt_1^2=v_0\sin\theta \cdot \frac{v_0}{g} \sin\theta-\frac{1}{2}g \left(\frac{v_0}{g} \sin\theta \right)^2 \)
　　\(\displaystyle =\left(1-\frac{1}{2} \right)\frac{v_0^2}{g} \sin^2\theta=\) \(\displaystyle \frac{v_0^2}{2g} \sin^2\theta \)

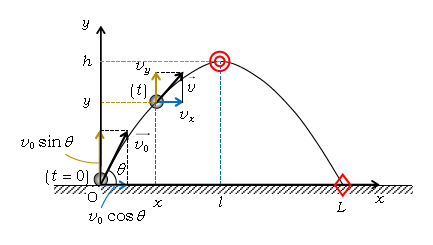
2⃣　落下点（図１の◇印）での時刻\(t_2\)、\(v_y\) 、\(x=L\)
　落下点では明らかに\(y=0\)
　すると\(\displaystyle y=0=y_0+v_{0y} t+\frac{1}{2}a_y t^2=0+v_0\sin\theta \cdot t_2-\frac{1}{2}gt_2^2 \)
　これは\(t_2\)に関する２次方程式で、変形すると　\(\displaystyle t_2 \left(\frac{1}{2}gt_2-v_0\sin\theta \right)=0 \)
　　∴　\(t_2=0、\) \(\displaystyle \frac{2v_0}{g}\sin\theta \)　[ ２次方程式なので解が２つ求まるが、\(t=0\)の解は小球の投げ出し時刻で\(y=0\)になっているという意味なので、解としては不適 ]
　ちなみに\(t_2=2t_1 \)になった。この意味の考察は次の単元1-15-3でやる。
　次に\(\displaystyle v_y=v_{0y}+a_y t=v_0\sin\theta-gt_2=v_0\sin\theta-g\frac{2v_0}{g}\sin\theta=\) \(-v_0\sin\theta\)
　これが初速度の\(y\)成分\(v_0\sin\theta\)の(-1)倍になっている意味の考察も1-15-3で。
　\(\displaystyle x=L=x_0+v_{0x} t+\frac{1}{2}a_x t^2=0+v_0\cos\theta \cdot t_2+0 \)
　　\(\displaystyle =v_0\cos\theta \cdot \frac{2v_0}{g} \sin\theta=\frac{v_0^2}{g}2\sin\theta\cos\theta= \)\(\displaystyle \frac{v_0^2}{g}\sin2\theta \)　
　[ 倍角の公式を用いた ]　

3⃣　初速度の大きさ\(v_0\)を一定に保ったまま、投げ出しの角\(\theta\)を10°,23°,84°のようにいろいろ変えていったときの\(L\)の最大値、つまり水平方向の到達距離の最大値、およびそのときの\(\theta\)
　2⃣で求めた\(\displaystyle L=\frac{v_0^2}{g}\sin2\theta \)で、\(\theta\)を変数と見なして\(L\)の最大値を求めるというもの。
　-1≦\(\sin2\theta\)≦1だから、\(\displaystyle L_{\text{max}}=\frac{v_0^2}{g} (\sin2\theta)_{\text{max}} =\frac{v_0^2}{g}×1=\) \(\displaystyle \frac{v_0^2}{g} \)
　また、\(\sin2\theta\)が最大値1をとるのは\(\sin\)の中身\(2\theta=90°\)のときだから、\(\theta=\) \(45°\)。
　低すぎる角度(例えば15°)で投げても、高すぎる角度(例えば75°)で投げても、\(L\)は大きい値にはならないが、程よい角45°で投げると最も遠くへ到達するという意味。

4⃣　軌跡の式
　軌跡の式とは\(x\)-\(y\)平面における関数関係\(y=f(x)\)を曲線表示したもの。次のようにして求める。
　\(x\)と\(t\) の関係式　\(x=v_0\cos\theta \cdot t \)　　　　　　(1)
　\(y\)と\(t\) の関係式　\(\displaystyle y=v_0\sin\theta \cdot t-\frac{1}{2}gt^2 \)　　(2)
から\(t\)を消去すれば、関数\(y=f(x)\)が得られて、それが軌跡の式になる。
　そこで(1)より得られる \(\displaystyle t=\frac{x}{v_0\cos\theta} \) を(2)に代入して\(t\)を消去する。
　　\(\displaystyle y=v_0\sin\theta \frac{x}{v_0\cos\theta}-\frac{1}{2}g \left(\frac{x}{v_0\cos\theta} \right)^2 \)
　　∴　\(\displaystyle y=\tan\theta \cdot x-\frac{g}{2v_0^2\cos^2\theta}x^2 \)
　これは\(x\)の2次の係数が負の2次関数だから、上に凸の放物線で、たしかに小球を空中に投げ出すと放物線を描く（図１）。
　ちなみに2次関数を平方完成すると、
　　\(\displaystyle y=-\frac{g}{2v_0^2\cos^2\theta} \left( x^2-\frac{2v_0^2\cos^2\theta}{g}\tan\theta \cdot x \right) \)
　　\(\displaystyle =-\frac{g}{2v_0^2\cos^2\theta} \left(x^2- \frac{2v_0^2}{g}\sin\theta\cos\theta \cdot x \right) \)
　　\(\displaystyle =-\frac{g}{2v_0^2\cos^2\theta} \left(x- \frac{v_0^2}{g}\sin\theta\cos\theta \right)^2+\frac{g}{2v_0^2\cos^2\theta} \left( \frac{v_0^2}{g}\sin\theta\cos\theta \right)^2 \)
　∴　\(\displaystyle y=-\frac{g}{2v_0^2\cos^2\theta} \left( x- \frac{v_0^2}{g}\sin\theta\cos\theta \right)^2 +\frac{v_0^2}{2g}\sin^2\theta \)
　これから軸\(\displaystyle x=\frac{v_0^2}{g}\sin\theta\cos\theta \)、頂点の\(\displaystyle y=\frac{v_0^2}{2g}\sin^2\theta \)であることが分かる。軸及び頂点は1⃣で求めた\(x=l\)、\(y=h\)に一致している。