1-04-1: 落体の運動

落体の運動は等加速度直線運動の代表例。計算の仕方をしっかり身に付けましょう！　→　＜例題＞は1-04-2へ　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　物理で「向き」を正確に表現するときは、「○○方向△△向き」という言い方をする。例えば「水平方向右向き」。「水平方向」というと右向き左向き両方を含む表現で、「水平方向右向き」で向きが１つに確定する。もちろん、単に「水平右向き」でも意味は通じる。「鉛直方向」とは地球の中心に向かう、あるいは中心から遠ざかる方向という意味。

　単元タイトルの「落体の運動」とは、物体を投げ上げたり、投げ下ろしたり、あるいは物体からそのまま手を離した場合の運動。それはポイントにまとめたように、
　　鉛直下向きの重力加速度\(g\)（≒9.8m/s\(^2\)）による鉛直方向の等加速度直線運動　　(＊)
である（ただし、空気抵抗を無視する）。この加速度には「重力加速度\(g\)」なる特別な名前が与えられている。(＊)のようになる理由はしばらく先の単元1-15-1で証明するとして、ここでは(＊)を重要事項としてとりあえず覚えてしまおう。さっそく練習として、小球を投げ上げる場合を考えることにする。
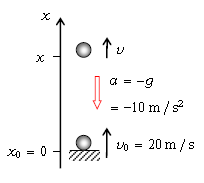
　地面の高さを原点とする、上向き正の\(x\)軸を取る。図１に初期条件\(v_0=\)20m/s、 \(x_0=\)0と書いてある。簡単のため、重力加速度\(g\)≒9.8m/s\(^2\) ≒10m/s\(^2\) とする。(＊)の通り\(g\)は下向きだが、上向きを(\(x\)軸の)正の向きに取ったので、加速度\(a\)はマイナスで\(a=-g=- \)10m/s。　[ 初めに≒10と言ったなら、次からはいちいち≒10(約10)と表記せずに、=10(正確に10)と書くのが慣習 ]

　まず、(1)式より
　\(v=20-10t \; \)　　　　　　(1′)
これを\(v\)-\(t\)グラフに表すには、縦軸\(v\)を数学の\(y\)のように読み、横軸\(t\)を\(x\)のように読んで、(1′)を(心の中では)
　\(y=20-10x \)
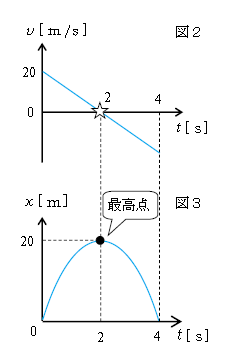
のように読むとよい。すると、縦軸切片20、傾き-10の直線の式であることが分かり、図２のような\(v\)-\(t\)グラフが書ける。

　次に(2)式より \(\displaystyle x=0+20t-\frac{1}{2} ×10t^2=-5t^2+20t=-5(t^2-4t) \)　平方完成して
　 \(x=-5(t-2)^2+20 \)　　(2′)
これを\(x\)-\(t\)グラフに表すために、縦軸\(x\)を数学の\(y\)、横軸\(t\)を\(x\)のように読んで、(2′)を
　 \(y=-5(x-2)^2+20 \)
のように読む。これは２次関数で、頂点が\( (2,20) \)の放物線だから、図３のような\(x\)-\(t\)グラフが書ける。
　図２から読み取れることは――
　0≦\(t\)<2では\(v\)>0、つまり図１の\(+x\)方向に動くから上昇し、2<\(t\)≦4では\(v\)<0、つまり\(-x\)方向に動くから下降する。\(v\)>0上昇から\(v\)<0下降に切りかわる\(v=\)0の所（図２中の☆）でいったん止まって、そこが最高点となるはず。たしかに図３を見ると、☆の時刻で最高点●になっている。
　\(v\)の符号が切りかわる点☆を、運動の折返し点（Ｕターンする所）という。言いかえると、\(v\)-\(t\)グラフが横軸をまたぐ所。これは落体の運動に限らず、\(v\)-\(t\)グラフの目の付け所としてとても重要だ。

1⃣  最高点に達する時刻\(t_1\)と最高点の高さ\(h\)　[ 答は以下の緑の下線部 ]
　最高点では\(v=\)0（図２☆）だから、(1)式より \(\displaystyle v=0=v_0-gt_1 \)
　　∴　\(t_1= \)\(\displaystyle \frac{v_0}{g} \)　（ ∴ という記号は「ゆえに」と読む。念のため。）
　(2)式に代入して 最高点の\(\displaystyle x=h=0+v_0t_1-\frac{1}{2} g{t_1}^2=v_0\frac{v_0}{g} -\frac{1}{2} g \left( \frac{v_0}{\textit{g}} \right)^2 \)
　　\(\displaystyle =\frac{{v_0}^2}{g} -\frac{1}{2} \frac{{v_0}^2}{g}= \)\(\displaystyle \frac{{v_0}^2}{2g} \)

2⃣  地面に落下する時刻\(t_2\)と落下点での速度\(v_2\)
　落下点では\(x\)=落下位置=0となるから、(2)式より
　　\(\displaystyle x=0=0+v_0t_2-\frac{1}{2} g{t_2}^2 \)
　　∴　\(\displaystyle {t_2}^2-\frac{2v_0}{g} t_2=0 \)　　∴　\(\displaystyle t_2
\left( t_2-\frac{2v_0}{g} \right)=0 \)
　\(t_2 \ne 0 \)だから 　\(t_2=\)\(\displaystyle \frac{2v_0}{g} \)
　(1)式に代入して　落下点の\(\displaystyle v_2=v_0-gt_2=v_0-g\frac{2v_0}{g}=\)\(-v_0 \)
　\(v_2\)<0と求まったということは、落下点で速度は負の向き(下向き)という意味で、これは妥当である。

　なお、いま\(t_2=2t_1\)、\(v_2=-v_0\)となっている。この意味付けについては1-15-3で扱う。