10-03-4: 電位の公式の導出

点電荷のつくる電位の公式$\phi=k\frac{Q}{r}$ を証明します！　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の $\equiv$ 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　電位$\phi$とは3-03-1の通り、1Cあたりの持つ位置エネルギーだから、位置エネルギーの定義(10-03-2)
　「ある位置から基準点まで保存力がすることのできる仕事」　　　　　　　　 (1)
から始めることにしよう。この定義は、重力による位置エネルギーなら「高さ$h$から高さ0の所(基準点)まで重力がすることのできる仕事(1-17-1)」(すなわち$mgh$)である。この単元で導出したいのは点電荷$Q$($Q≷0$)のつくる電位(1Cあたりの持つ位置エネルギー)$\phi$の公式で、この場合、基準点を無限遠に取るのが慣習だから（理由は最後に述べる）、電位の定義は(1)にならって
　「点電荷$Q$の位置より距離$r$へだてた位置から、無限遠(基準点)まで、1Cあたりの電気力のすることのできる仕事」
となる。ところが、1Cあたりの電気力とは電場(3-02-1)に他ならないから、結局電位$\phi$とは、
　「$Q$より距離$r$へだてた位置から無限遠まで電場$\vec{E}$のすることのできる仕事」$\:$ (2)
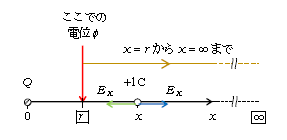
として求まる。この計算をするために、図１のように$Q$の位置を原点Oとする$x$軸を取り、任意の位置$x$に+1C及び電場の$x$成分$E_x$を書く。
　電場$\vec{E}$の向き(3-02-1)は、$Q>0$なら$Q$から+1Cへの斥力の向きで$E_x>0$(青い矢印で$+x$方向)、$Q<0$なら$Q$から+1Cへの引力の向きで$E_x<0$(緑の矢印で$-x$方向)（もちろん$E_y=0$）　 (☆)

　ここで3-02-1より　$\displaystyle E_x=k\frac{Q}{x^2}\:$　　　　　　　　　　　　　　　　　　　　(3)
(3)で$Q≷0$なら$E_x≷0$（複合同順）なので、(☆)に述べたことと合っている。　
　さて、(3)の$E_x$(1Cあたりに働く力)は$x^2$に反比例で、一定ではない。ゆえに、仕事$W=$(力の移動方向成分)×(距離)(1-16-1)とすることはできない。そこで、力の移動方向成分$F$が変化していく場合の$F$のする仕事=$F$-$x$グラフの面積　の考え方(1-18-1)を用いて、
　$E_x$(1Cあたりに働く力)のする仕事=$E_x$-$x$グラフの面積　　　　　　　
と計算することにする。ということは、
　(2)の電位$\phi$=（$Q$より距離$r$へだてた位置から無限遠まで電場$\vec{E}$のする仕事）
　　　　　　 =（$x=r$から$x=\infty$まで$E_x$-$x$グラフの囲む面積）$\;\:$　　　　　(4)
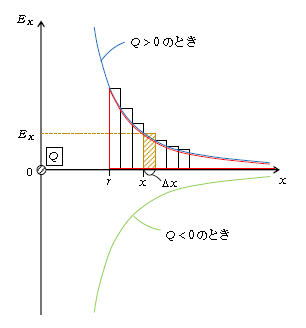
　図２に$E_x$-$x$グラフを示した。(3)の通り$x^2$に反比例、青い曲線が$Q>0$で$E_x>0$のグラフ、緑の曲線が$Q<0$で$E_x<0$のグラフである。(4)の面積を、$Q>0$の場合について赤色で囲ってある。　[ $F$-$x$グラフや$v$-$t$グラフの単元の説明通り、赤く囲まれたグラフの面積を、横幅の微小な長方形のいくつもの連なりで置き換える階段グラフ(の一部)を示してある。斜線を施した長方形の面積は$E_x$(1Cあたりに働く力)×$\Delta x$だから、(1Cあたりの)微小仕事を表している。]　
　ところで、グラフの面積は定積分で表せる。(4)の定積分は具体的には、積分の中身(被積分関数)を縦軸の量$E_x$、積分変数を横軸の量$x$($dx$)、積分の下端・上端をそれぞれ$x=r,\,\infty$として、
　電位$\displaystyle \phi=\int_{r}^{\infty}E_xdx$　[ (3)を代入 ]　=$\displaystyle \int_{r}^{\infty}k\frac{Q}{x^2}dx\,$　　　　　　　　　　(5)

　(5)で$Q<0$のとき$\phi<0$であるが、このとき(1Cあたりの)力$E_x$は負の向き($E_x<0$)、移動の向き($x=r$から$x=\infty$)は正の向き、つまり力の向きと移動の向きが逆だから、負の(1Cあたりの)仕事(1-16-1)、すなわち$\phi<0$となり適している。
　(5)より　$\displaystyle \phi=kQ\int_{r}^{\infty}\frac{1}{x^2}dx=kQ\left[-\frac{1}{x}\right]_{r}^{\infty}=kQ\left(-\frac{1}{\infty}+\frac{1}{r}\right)$　　(6)
　$\displaystyle \frac{1}{\infty}→0$なので　$\displaystyle \phi=k\frac{Q}{r}$　　　　　　　　　　　　　(＊)
　これが3-03-1で用いた点電荷のつくる電位$\phi$の公式である。

　ポイントすぐ下の初めの段落で「基準点を無限遠に取る」といった理由が、この時点でハッキリする。仮に無限遠$x=\infty$ではなく、どこか有限の位置$x=r_0$を基準に取ると、(5)の積分は
　$\displaystyle \phi=\int_{r}^{r_0}k\frac{Q}{x^2}dx$　となる。すると(6)の計算は
　$\displaystyle \phi=kQ\int_{r}^{r_0}\frac{1}{x^2}dx=kQ\left[-\frac{1}{x}\right]_{r}^{r_0}=kQ\left(-\frac{1}{r_0}+\frac{1}{r}\right)$　となり、電位の公式がいかにも覚えづらい式$\displaystyle \phi=kQ\left(-\frac{1}{r_0}+\frac{1}{r}\right)$　となってしまう。そう、点電荷のつくる電位の基準点を無限遠に取る理由は、公式を覚えやすくする( (＊) )単なる便宜上なのである。