5-07-1: 熱力学第１法則

熱力学第１法則はエネルギー保存則、その意味をきっちり理解しましょう！　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

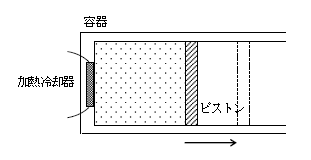
　図１のように、シリンダー容器内の気体を外に漏らさず容器の内側面をなめらかに動くピストンがある。容器の底面には気体を加熱も冷却もできる加熱冷却器が取り付けてある。容器及びピストンは断熱材で覆われており、容器内の気体と外気の間での熱の移動は無視できるとし、容器、加熱冷却器及びピストンの熱容量も無視する。
　いま、加熱冷却器で気体に熱量\(Q\)を与えるとピストンが右へ移動した。この過程で気体は外部に仕事\(W\)をし、気体の内部エネルギー\(U\)が\(\Delta U\)だけ変化したとする。気体とピストンを系と見なすと、系の外から内へ熱量\(Q\)の分だけエネルギーが流入し、内から外へ仕事\(W\)の分だけエネルギーが流出し（5-06-1の参考で、気体が外部にした仕事は系外へのエネルギー移動分になることを説明した）、系内のエネルギーが\(\Delta U\)変化したことになる。　　(☆)
　一般的にエネルギー保存則は、(系外から流入するエネルギー)
　　　　＝(系内のエネルギー変化)＋(系外へ流出するエネルギー)　　　(1)
の形で書ける。というのも、例えば外から70 J 入ってきて、外へ40 J 出ていったときに、内が30 J 増加したなら自然界のエネルギーは「行方不明」になっていないが、内が20 J しか増加しないと10 J だけ自然界のエネルギーが消失しているからだ。エネルギーをお金に見立てて、(1)を「収入＝たくわえ＋消費」のように理解するのも悪くない。

　さて、気体とピストンを系と見なすと、外圧に逆らってした仕事に関する5-06-1の説明が呑み込みやすかったはずだ（そもそも外圧は気体ではなくピストンに加わっている）が、「気体とピストン」と言うのはいかにも煩わしい。そこで、気体とピストンを系にする場合、これ以後は単に「気体を系とする」と表現する。(☆)の内容を(1)に当てはめると、
　　　\(Q \; \)　　　 \(=\)　　　 \(\Delta U\)　　　　　\(+\)　　　 \(W\)　　　　　　　　　 (2)
　　気体の　　　|　　　気体の　　　　　|　　気体が
　吸収した熱量　|　内部エネルギー変化　|　外部にした仕事
これを熱力学第１法則という。４点補足しよう。

1⃣　第１法則はエネルギー保存則である。ところで、5-01-1の通り熱量とは、熱運動（無秩序な乱雑な分子レベルの運動）のエネルギーの移動量だから、アボガドロ数程度(10\(^{23}\))の分子運動に関わる量で到底計算不可能である。ということは、第１法則を導出することは事実上できない。ではなぜこの法則が成り立つのかと聞かないでほしい。むしろ我々の宇宙は第１法則が成り立つようにできているという仮説を置いて、それが実験事実を見事に説明するから、第１法則は成り立つと認めているのである。この法則の成り立たないまた別の宇宙があるのかもしれないが、そんな宇宙があるかどうかの答は現在の物理学にはない。ともかく我々の宇宙においては、第１法則を熱力学の出発点の式として認めよう。この出発点の式という意味において第１法則は、熱力学における「宇宙の根本原理」(1-05-1,3-01-1)である。

2⃣　熱力学第１法則(2)に現われる\(Q,\Delta U,W\)の単位は全て[J]。ここで唐突なことを言うようだが、厳格な物理用語の使い方としては、各状態ごとに定義可能な量しかエネルギーと呼んではいけない(!)。内部エネルギー\(U\)はもちろんエネルギーと呼べる。初めの状態の温度\(T_{まえ}\)が決まれば単原子分子気体の\(U=\frac{3}{2} nRT_{まえ}\)（5-04-3）が決まり、終りの状態の温度\(T_{あと}\)が決まれば\(U=\frac{3}{2} nRT_{まえ}\)が決まり、途中の任意の状態でもことごとく\(U\)は定義可能だからだ。ところが、\(Q_{まえ}\)は存在しない。というのも1⃣の通り、熱量\(Q\)とはまえからあとにおける[J]単位の量の移動分だからである。\(Q_{あと}\)も存在しない。つまり熱量はエネルギーとは呼べず、厳密には「エネルギーの移動量」と呼ぶべき量である。同様に\(W_{まえ}\)や\(W_{あと}\)は存在せず、むしろ、まえからあとの間に〇〇[J]仕事をしたという表現をすることから分かる通り、仕事もエネルギーとは呼べない。気体が外部にする仕事は、系内から系外への「エネルギーの移動量」である。

3⃣　1⃣の通り熱量\(Q\)は到底計算不可能である。ところが、仕事\(W\)は\(W=\)(\(P\)-\(V\)グラフの面積)（5-06-1）のように計算可能。内部エネルギー変化\(\Delta U\)も単原子分子気体については\(\Delta U=\Delta(\frac{3}{2} nRT) \)（5-04-3）のように計算可能。すると(2)を用いて、計算が絶望的に思えた熱量\(Q\)が求まるという意義が熱力学第１法則にはある。つまり、第１法則の使い方はほとんどの場合、\(\Delta U\)を計算して\(W\)を計算すると未知量の\(Q\)が求まるというもの。ただし、断熱変化では例外的に、断熱であるがゆえにハナから\(Q=0\)と決まっており、\(Q\)は未知量ではない。

4⃣　加熱冷却器で気体から熱を奪う、すなわち(2)で気体が熱量を放出する放熱の場合は、\(Q=-50\) J のように吸熱\(Q<0\)として扱えばよい。気体が仕事をされる場合は、\(W=-80\) J のように、した仕事\(W<0\)として扱えばよい（5-06-1の通り、された仕事\(=(-1)\)×した仕事）。
　なお、問題で「放熱量\(q\) はいくらか」のように聞かれたら、吸熱量\(Q<0\)を(2)を用いて計算し\(q=|Q|\)とその大きさを答えるのがよい。「された仕事\(w\) はいくらか」と聞かれたら、した仕事\(W<0\)を計算し\(w=|W|\)と大きさを答えるのがよい。