5-04-3: 気体分子運動論 #その3
分子運動論の三部作(I)(II)(III)を全てまとめます! → <#その1>は5-04-1、<#その2>は5-04-2へ
ポイント(I) 5-04-2のまとめです。
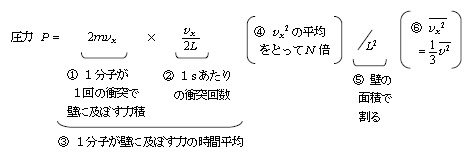
上の式の分子には\(2m\overline{{v}^2}×N \)があり [④、⑥に注意 ] 、分母には\(2L^3×3\)がある。よって、5-04-2の結論 \(\displaystyle P=\frac{Nm\overline{v^2} }{3V}\) が得られる。マクロな\(P\)をミクロな\(m,v\)で表した分子運動論さながらの式だ。この式は覚えられればそれに越したことはないが、覚えるだけでは問題は解けない。なぜなら、入試では①から⑥のそれぞれが小問で問われる対象となるから。そのつもりでポイント(I)の①から⑥それぞれ、及び全体の話の流れをしっかり押さておこう。
(II) 気体分子の平均運動エネルギー
ポイント(II) 気体分子の平均運動エネルギー \(\displaystyle \overline{\frac{m}{2} v^2}=\frac{3}{2} kT \)
\(k\): ボルツマン定数=1.4×10\(^{-23}\) J/K
\(\displaystyle k=\frac{R}{N_A}\) (\(R\): 気体定数、\(N_A\): アボガドロ数)なる関係がある。
5-01-1で温度とは熱運動の激しさの度合いであると述べた。分子運動論的には、熱運動の激しさの指標として分子の平均運動エネルギーを取り、それが絶対温度に比例すると定める。ただし、エネルギーの単位は[J]、絶対温度\(T\)の単位は[K]だから、[J/K]の単位を持つボルツマン定数\(k\)を導入して
\(\displaystyle \overline{\frac{m}{2}{v_x}^2}=\overline{ \frac{m}{2}{v_y}^2}=\overline{\frac{m}{2}{v_z}^2}=\frac{1}{2}kT \) (エネルギー等分配則という) (1)
を分子運動論の枠組みにおける絶対温度の定義として採用する。(1)は5-04-2の⑥で登場した式
\(\overline{{v_x}^2}=\overline{{v_y}^2}=\overline{{v_z}^2} \) とつじつまが合う。
(1)を温度の定義式とする妥当性の1つは、(1)から実験的経験則としての状態方程式\(PV=nRT\)が直接導けることにある。
証明 5-04-2の⑤の式\(\displaystyle P=\frac{Nm\overline{{v_x}^2} }{V} \) すなわち \(PV=Nm\overline{{v_x}^2} \) に
(1)から得られる\(\overline{m{v_x}^2}=kT \) を代入 \(PV=NkT \)
ここで、分子数\(N=\)1molあたりの分子数(アボカドロ定数)\(N_A\)×モル数\(n\) (2)
であるから \(PV=N_AnkT=n\cdot N_A k \cdot T \)
\(N_A k=R\) と書くと \(PV=nRT \) よって状態方程式が導けた。
のみならず、\(\displaystyle k=\frac{R}{N_A} \; \) (3)
の関係があることも分かった。
さて、(1)に5-04-2の⑥のもう1つの式 \(\displaystyle \overline{{v_x}^2}=\frac{1}{3}\overline{v^2} \) を代入すると、ポイント(II)の式
気体分子の平均運動エネルギー \(\displaystyle \overline{\frac{m}{2} v^2}=\frac{3}{2} kT \) (4)
が得られる。これは(1)と同様、事実上温度の定義式だから覚えよう。(4)式の言っている内容としては、
温度\(T\)が高いほど分子の平均運動エネルギーは大きい。
温度\(T\)が等しければ、気体の種類によらず分子の平均運動エネルギーは等しい。
同じ温度\(T\)では軽い分子ほど速く、重い分子ほど遅く運動する。 (#)
(II)に関連して、\(\sqrt{\overline{v^2}} \) [m/s] を2乗平均速度という。(4)より
\(\displaystyle \sqrt{\overline{v^2}}=\sqrt{\frac{3}{m}kT}=\sqrt{\frac{3}{m}\frac{R}{N_A}T} \) < (3)を用いた >
また、\(mN_A=\)分子の質量×アボガドロ定数(1molあたりの分子数)\(=\)分子1molの質量
\(=\)分子量\(\mu\)×10\(^{-3}\)[\(\text{kg}\)] だから \(\displaystyle \sqrt{\overline{v^2}}=\sqrt{ \frac{3RT}{\mu×10^{-3}} } \)
青の下線部は覚えるというよりも、その式変形を練習しておくとよい。また(#)に関連して、非常に軽いH\(_2\)分子は2乗平均速度が約1800m/s、比較的重いCO\(_2\)分子は約400m/s 、つまり気体分子の速さはざっと500m/sである。
(III) 単原子分子気体の内部エネルギー
ポイント(III) 単原子分子気体の内部エネルギー
\(\displaystyle U=N \cdot \overline{\frac{m}{2}v^2}= N \cdot \frac{3}{2}kT=\frac{3}{2}nRT=\frac{3}{2}PV \)
単原子分子気体とは、文字通り1個の原子が分子を成す気体のことで、周期表の一番右に位置するHe, Ne, Ar, Kr, Xe, Rn (不活性ガス)だ。内部エネルギーとは簡単に言うと次のような量である ―― たとえ気体全体が静止していて一見エネルギーがないように見えても、分子各々は運動しているのであってエネルギーを持っている。こうした気体の内部に隠されているかのようなエネルギーのことを内部エネルギーという(内部エネルギーの詳しい話は5-08-1で扱う)。
ということで、単原子分子気体の内部エネルギー\(U\)=分子各々の運動エネルギーの総和 となる。すると、
\(\displaystyle U=N \cdot \overline{\frac{m}{2}v^2} \) < (4)を用いて >
\(\displaystyle =N \cdot \frac{3}{2} kT\) < (3)(2)を用いて \(\displaystyle Nk=N\frac{R}{N_A}=\frac{N}{N_A}R=nR\) と変形できるから >
\(\displaystyle =\frac{3}{2}nRT \) < 状態方程式を用いて >
\(\displaystyle =\frac{3}{2}PV \)
内部エネルギーは出題率が極めて高いから、ポイント(III)の等式は全て頭に入れておこう。
特に\(U=\frac{3}{2}nRT \)の表式を見ると、モル数\(n\)が大きいほど、温度\(T\)が高いほど、\(U\)が大きい。この意味は次のように理解できる ―― まず\(n\)が大きいということは、分子数\(N\)が大きいということ。\(N\)が大きいほど内部に隠されているかのような\(U\)は大きい。また\(T\)が高いということは、(4)より1分子の平均運動エネルギーが大きいということ。1分子のエネルギーが大きいほど内部に隠されているかのようなエネルギー\(U\)は大きい。


