5-06-1: 気体が外部にする仕事
ポイント下の第1段落をしっかり読みましょう!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 気体が外部にする仕事\(W\)=気体が外圧\(P_外\)に逆らってする仕事
・ ピストンが「ゆっくり」動く場合は\(W\)=気体の圧力\(P\)がする仕事
\(P\)が一定の場合 \(W=P\Delta V \) (\(\Delta V\): 体積\(V\)の変化量)
\(P\)が一定でない場合は \(W=\)(\(P\)-\(V\)グラフの面積)
膨張なら\(W>0\)、収縮なら\(W<0\)
・ \(V\)が一定の場合 \(W=0 \)
・ 気体が外部からされた仕事\(W’\)=気体が外圧によってされた仕事
=\((-1)×\)気体が外部にした仕事\(W\)
図1のように、シリンダー容器内の気体を外に漏らさず容器の内側面を水平方向になめらかに動くピストンがあるとし、ピストンの壁の面積を\(S\)とする。気体が壁に圧力\(P\)すなわち力\(PS\)を加えつつ、壁を距離\(\Delta x\)移動させる場合を考えよう。ここで気体とピストンを系と見なしたとき、系外から加わる単位面積あたりの外力を外圧\(P_外\)という。外力としては、大気圧による力、人がピストンに加える力、ばね付きピストンならばばねの弾性力、…などいろいろ想定できる。このとき気体の圧力\(P\)と外圧\(P_外\)はつり合っている必要はない。例えば\(P>P_外\)ならピストンは半ば勢いよく右に移動する。容器内の気体には流れのエネルギーが生じる。ところが、である。このエネルギーは流体力学(大学の課程)的エネルギーなので、高校物理では扱えない。そこで高校では、多くの場合「準静的過程」 ―― ピストンがほぼつり合いを保ちながらきわめてゆっくり動く過程を扱う。問題文中に「ゆっくり」というキーワードがあったなら、それは準静的過程を考えるという意味だ。
準静的過程では\(P=P_外\)と見なせる。このとき「気体が外部にする仕事」を気体の圧力\(P\)のする仕事と捉えることに問題はない。しかし、\(P \ne P_外\)の一般の場合、気体が外部にする仕事の定義は気体が外圧\(P_外\)に逆らってする仕事(外圧\(P_外\)と同じ大きさで逆向きの圧力のする仕事、つまり\(P\)とは関係がない)である。 (☆)
なぜこのように定義するのかの話を冒頭からすると細かくなりすぎるので、この単元最後の参考に回す。
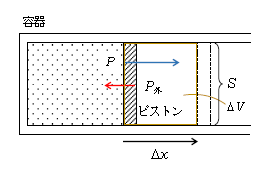
では準静的過程を扱っていく。まず\(P\)が一定の定圧変化では、図1より気体が外部にする仕事\(W=\)力\(PS×\Delta x \) 。ここで気体の体積\(V\)の変化量\(\Delta V=S\Delta x \)だから、\(W=P\Delta V \)
\(\Delta V>0 \)(膨張)のとき\(W>0\)である一方、\(\Delta V<0 \)(収縮)のとき\(W<0\) 。その意味は、\(\Delta V<0 \)のときは図1の\(\Delta x \)が左向きとなり、力\(PS\)の向きと移動\(\Delta x \)の向きが逆のとき仕事は負ということである。
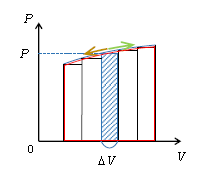
次に\(P\)が一定でない一般の場合は、1-02-1,1-18-1,3-08-2など様々な場面で利用してきた階段グラフの考え方を用いる。図2の青い長方形の面積は\(P\Delta V \)だから微小仕事\(\Delta W\)を表す。気体が外部にする仕事\(W\)は微小仕事の総和すなわち階段グラフの面積で、\(\Delta V → 0\)の極限をとるとグラフの面積(赤)に一致する。よって
\(W=\)(\(P\)-\(V\)グラフの面積)
なお\(P\)とは圧力の「大きさ」という意味なので、\(P\)-\(V\)グラフが横軸の下側に書かれることはない。仕事の正負は横軸の移動方向で決まる、つまりグラフを右にたどる膨張(緑の矢印)のときは\(W>0\)で、左にたどる収縮(黄色の矢印)のときは\(W<0\)である。これは、1-02-1で述べた「横軸の下側では\(v\)-\(t\)グラフの面積を\((-1)\)倍すると変位に等しくなる」とは事情が異なるので注意しよう。
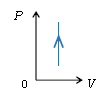
一方、\(V\)が一定の定積変化では、\(P\)-\(V\)グラフが右のようになってその面積が0、すなわち仕事\(W=0\)。定積変化は図1の例では、ピストンが動かず移動距離\(\Delta x =0\)の場合に相当する。距離が0なので仕事\(W\)も0だ。
「気体が外部からされた仕事」\(W’\)の定義は気体が外圧によってされた仕事である。これは、準静的過程でもそうでなくても気体が外圧に逆らってした仕事のピッタリ\((-1)\)倍だから、(☆)より必ず
気体が外部からされた仕事\(W’=(-1)×\)気体が外部にした仕事\(W\) となる。
参考 なぜ(☆)のように気体が外部にする仕事を定義するのか説明しよう。簡単のためピストンの質量を無視する。3-09-1で「系外から仕事を加えると、その分だけ系内のエネルギーが変化する」という、半ばエネルギーに関する宇宙の根本原理について述べた。ここで、系外を1つの系と見なせば、次のことが言える:「系外に仕事を加えると、その分だけ系外のエネルギーは変化する」あるいは「系外に加えた仕事が系外へのエネルギー移動分になる」。ポイントすぐ下の段落で述べたように気体とピストンを系と見なすと、「外圧に逆らってする仕事が系外へのエネルギー移動分になる」。 (*)
例えばばね付きピストンならば、ばねの弾性力に逆らってする仕事がばねの弾性エネルギーとなって移る。
さて、(1) \(P=P_外\)なら、ピストンはほぼつり合いを保ちつつきわめてゆっくり動くから、容器内の気体に流れのエネルギーは生じない。このとき(*)より、\(P_外\)に逆らってする仕事が系外へのエネルギー移動分になる。
(2) \(P>\)((1)と等しい)\(P_外\)なら、気体に流れのエネルギーが生じる。ピストンの質量\(M\)は無視したからその運動エネルギー\(\frac{M}{2}v^2\)は考えなくてよい。このときも\(P_外\)に逆らってする仕事が系外へのエネルギー移動分になる。
(1)と(2)を比べると、\(P>P_外\)の場合、気体の圧力\(P\)のする仕事と外圧\(P_外\)に逆らう仕事の差が、気体に生じた流れのエネルギーに等しいことが分かる。
ところで熱力学第1法則を立式するときは、5-07-1で説明するように、気体が外部にする仕事を「系外へのエネルギー移動分」と定義しておきたい。よって、(*)より気体が外部にする仕事\(W\)を、気体が外圧\(P_外\)に逆らってする仕事と定義するのである。(\(W\)を気体の圧力\(P\)のする仕事と定義するなら、\(W\)は系外へのエネルギー移動分と系内の流れのエネルギーとの和になってしまう。)


