3-03-1: 電位
目に見えずにイメージしづらい電気現象を明快に解説していく招待状第2弾です。 → 3-02-1電場と電気力線 が第1弾、3-04-1等電位線 ; 電場と電位差の関係 が第3弾(3-03-2電場と電位 <例題1>、3-03-3<例題2>もあり)
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 電位\(\phi \)=1Cあたりの持つ電気力による位置エネルギー[J/C=V]
点電荷\(q\)の持つ電気力による位置エネルギー\(U=q\phi \)
・ 点電荷\(Q\)のつくる電位\(\displaystyle \phi =k \frac{Q}{r}\)
\(Q\): 電気量[C]、\(r\): 電荷\(Q\)からの距離[m]、\(k\): クーロンの法則の比例定数
・ 電気力線の向きに電位は下がる
この単元の電荷とは、大きさの無視できる点電荷を指す。
ここで、いきなり力学的エネルギー保存の法則を持ち出す。運動エネルギーと位置エネルギーの合計を力学的エネルギーといい、それが一定のままであるという法則。つまりものが速くなって運動エネルギー\(\frac{m}{2} v^2\)が増えれば、位置エネルギーは減るし、遅くなって運動エネルギーが減れば位置エネルギーは増える。
例えば重力だけを受けてものが運動するときは、速くなると重力による位置エネルギー\(mgh\)は減るから高さ\(h\)が減る。つまり速くなるときはものは下降する(図1)。
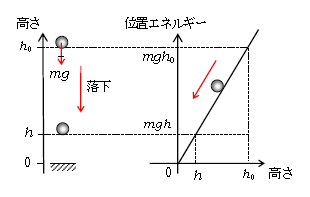
運動エネルギーが増えて速くなる
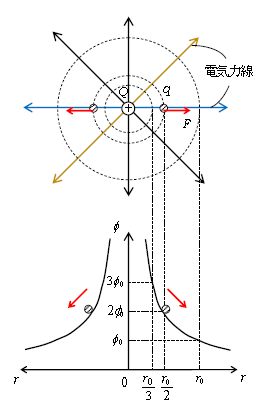
今度は電荷\(Q\)(>0)のまわりの電場中に別の電荷\(q\)(>0)を持ち込んだ場合(図2)。電気力線の向きに電荷\(q\)は電気力\(F\)を受けて、中央にある\(Q\)から遠ざかる向きに加速、その運動エネルギーを増やす。すると結論を先に言えば、何と「電気力による位置エネルギー」なる量が存在して、それが図2の下段のグラフのように両側へ行くにつれて減るのだ。グラフの縦軸横軸はこれから説明するとして、その前に今一度図1と2のグラフの概形を見比べておいてほしい。
さて、1-17-1でやった通り、重力による位置エネルギーの定義は「(基準点からの高さ\(h\)の所にある物体に対して)基準点まで重力がすることのできる仕事」だった。同様に電気力による位置エネルギーも「基準点まで電気力がすることのできる仕事」として定義できるが、電磁気分野では特に(\(q\)=)1Cあたりの持つ電気力による位置エネルギーを導入して、略して「電位\(\phi \)」(電位\(V\)という文字もしばしば用いられる)という。
電位\(\phi \)=1Cあたりに対して基準点まで電気力がすることのできる仕事 (*)
1Cあたりの持つ位置エネルギーが\(\phi \)ということは、2Cだったら位置エネルギー2×\(\phi \)を持ち、3Cなら3×\(\phi \)、…、ということで
\(q\)[C] の持つ位置エネルギー\(U=q×\phi \) である。
ここで\(\phi \)の公式を求めるためには定義(*)に従って仕事を計算してやればいいのだが、その計算はこの単元では省略、10-03-4に回す。10-03-4が一見して難しすぎると感じたなら、とりあえず以下の(☆)の公式を覚えてその使い方に慣れておけば差し当たり問題はない。しばらくしたら10-03-4にまた戻ろう。その公式が
\(\displaystyle \phi =k \frac{Q}{r}\) (☆)
である。電気力\(F\)が距離\(r\)の2乗に反比例なのに対し、電位\(\phi \)は距離\(r\)の1乗に反比例する形であることに注意しよう。繰り返すが、(☆)はとりあえず覚えるべし。
では図2のグラフの説明に入ろう。横軸は図2上段の青い電気力線に沿って測った、\(Q\)からの距離\(r\)を表す。横軸は右へ行っても左へ行っても\(r\)が増す。縦軸は電位(1Cあたりの持つ位置エネルギー)\(\phi \) 。横軸が\(r_0\)のときの縦軸は、(☆)より\(\displaystyle \phi_0=k \frac{Q}{r_0}\) 。\(\phi \)は\(r\)に反比例だから、横軸が\(\displaystyle r_0,\frac{r_0}{2},\frac{r_0}{3},\cdots \)と減っていくと、縦軸は\(\phi_0,2\phi_0,3\phi_0,\cdots \)と増えていく。なお、距離\(r\)を図2上段の黄色い電気力線に沿って測っても、上下に伸びる黒い電気力線に沿って測っても、グラフは全て同じになる。このように電荷\(Q\)のまわりの電場中には電位(1Cあたりの持つ位置エネルギー)\(\phi \)の高低の分布ができるから、「電荷\(Q\)のつくる電位\(\phi \)」という言い方をする。
位置エネルギー\(U\)の単位は[J]だが、電位\(\phi \)は1Cあたりの持つ位置エネルギーだから単位は[J/C]で、それを[V](ボルト)ともいう。
結局のところ、電位とは何かを一言で表すなら「高さ」である。ただし、それは[m]単位の空間的な高さのことではなく、[J/C]単位のエネルギー的高さである。図2の青い電気力線に沿って空間的高さは変わらなくても、電位は低くなっていく。つまり電位とは、あくまでもグラフの中での高さであると言ってもいいし、人間の頭の中でしかイメージできない高さであると言ってもいい。[ 図2のような2次元(\(x\)-\(y\))平面の電気力線に対しては、紙面と垂直に(\(z\)軸同様の)電位\(\phi \)軸を取って、エネルギーの高い低いをイメージできる。ただし、電気力線は実際には3次元(\(x\)-\(y\)-\(z\))空間に描かれているので、その各点各点に、エネルギーの高い低いを表す電位\(\phi \)を想定するということなのである。 ]
****************
| 3-02-1の通り、電荷\(Q\)が周りに 電場\(\vec{E} \)をつくり \(\Longrightarrow \) | その電場\(\vec{E} \)が他の電荷\(q\)に 電気力\(\vec{F}=q\vec{E} \)を及ぼす。 |
| 同様に、電荷\(Q\)が周りに 電位\(\phi \)をつくり \(\Longrightarrow \) | その電位\(\phi \)が他の電荷\(q\)に 位置エネルギー\(U=q\phi \)を持たせる。 |
****************
次に\(-Q\)<0の場合が図3。中央にある負電荷\(-Q\)は正電荷+1Cに引力\(F\)を及ぼすから、+1Cは\(-Q\)に近づく向きに加速、その運動エネルギーを増やす。ということは\(-Q\)に近づけば近づくほど電位\(\phi \)(+1Cあたりの持つ位置エネルギー)が減る。横軸が\(r_0\)のときの縦軸は、(☆)より\(\displaystyle \phi=-\phi_0=k \frac{-Q}{r_0}\)<0であることに注意。負電荷\(-Q\)のつくる電位\(\displaystyle \phi =k \frac{-Q}{r}\)は負だ。
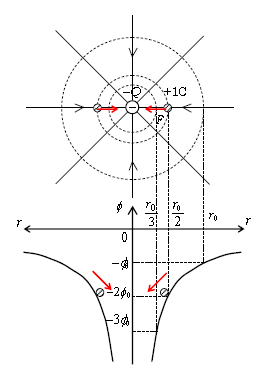
まとめると、\(Q\)>0のつくる電位は(無限に)高い山のイメージ、\(-Q\)<0のつくる電位は(無限に)深い谷のイメージである。
また、次のことも言える ―― 3-02-1でやった通り、電気力線の向きは電場\(\vec{E} \)(1Cあたりの力)の向き、電場の向きに速さが増え、運動エネルギーが増えて、位置エネルギーは減る、電位(1Cあたりの位置エネルギー)が減る。よって電気力線の向きに電位は下がるのだ。
→ 3-02-1電場と電気力線 が第1弾、3-04-1等電位線 ; 電場と電位差の関係 が第3弾(3-03-2電場と電位 <例題1>、3-03-3<例題2>もあり)


