3-01-1: 電気分野の準備
まずは電磁気の基本中の基本からスタートしましょう!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント ・ クーロンの法則
| 何から働く | 向き | 大きさ | |
| 電気力 または クーロン力 | 電荷どうし で働く | 同符号の電荷どうしは斥力 逆符号の電荷どうしは引力 | 以下の 通り |
力の大きさ\(\displaystyle F=k\frac{|q_1 q_2|}{r^2} \)
\(q_1, \, q_2\): 電気量[C] \(r\): 2電荷間の距離[m]
\(k\): (真空中の)クーロンの法則の比例定数=9.0×10\(^9\)[N\(\cdot \)m\(^2\)/C\(^2\)]
\(F\)は2電荷の積\(|q_1 q_2|\)が大きいほど、
2電荷の距離\(r\)が小さいほど、大きい
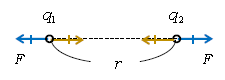
逆符号のときは引力(黄色の矢印)
・ 電流\(I\)=注目断面を1sあたり通過する電気量[A]
注目断面を微小時間\(\Delta t\)の間に通過する電気量\(\Delta q\)=電流\(I\)×時間\(\Delta t\)
物質は質量 \(m\)[\(\text{kg} \)]という性質を持っているだけでなく、電気量あるいは電荷 \(q\)[C](クーロン)という性質も持っている。\(m\)にはプラスの値しかないが、\(q\)にはプラスもマイナスもある。プラスの電気量を正電荷といい、プラスの電気量を持った微粒子のことも正電荷という。
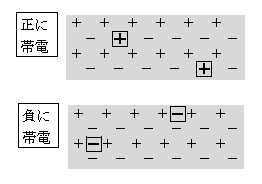
電気回路で用いる導線は、金属(主に銅)でできている。金属は無数の正電荷(金属正イオン+)と無数の負電荷(自由電子-)から成る(図1)。通常、金属中では+と-が同数かつ一様に分布していて、合計すると電気量0 。この状態を電気的に中性という。+やーどうしの距離は10\(^{-10}\)m程度とひじょうに小さく、+やーの個数はざっと10\(^{20}\)個程度とぼう大な数に上る。

一方、何らかの理由で+過剰の部分ができたなら、その部分は正に帯電しているといい、-過剰の部分は負に帯電しているという(図2)。
+や-の間には電気力\(F\)が働く(図3)。
同符号どうし(+と+、-と-)は、お互いを作用反作用で遠ざけ合う(斥力あるいは反発力、図中の青)。例えば左の+が右の+に右向きの力を及ぼすと、右の+が左の+に左向きの力を及ぼし返す。
逆符号どうし(+と-、-と+)は、お互いを作用反作用で引き合う(引力、図中の黄色)。例えば左の+が右のーに左向きの力を及ぼすと、右のーが左の+に右向きの力を及ぼし返す。

電気力あるいはクーロン力にはポイントにまとめたクーロンの法則が成り立つ。なぜか、と聞かないでほしい。むしろ、我々の宇宙はそれが成り立つようにできているという仮説を置いて、それが実験事実を見事に説明するから、クーロン則は成り立つと認めているのである。それの成り立たないまた別の宇宙があるのかもしれないが、そんな宇宙があるかどうかの答は現在の物理学にはない。ともかく我々の宇宙においては、クーロン則を電気分野の出発点の式として認めよう。この出発点の式という意味においてクーロンの法則は、電気分野における「宇宙の根本原理」である。つまり、クーロン則は覚えなければいけない。この段落で述べたことは、1-05-1の運動方程式についての説明と全く同様である。
なお、正確には、クーロンの法則は大きさを無視できる「点」電荷について成り立つ。[ また、深入りはしないが、次の単元3-02-1で扱うクーロン「電場」に関する法則を宇宙の根本原理と見なすのがむしろ自然であることが、3-02-1を読んだ後では分かるだろう。 ]
さて、電流が流れるときには、金属の性質により無数の-(自由電子)が全体として平行移動していく。+(金属正イオン)は金属全体を構成するいわば枠組みとして全体として静止している。しかし図4の通り、-の流れとそれと逆向きの+の流れは同値。そこで普通は、電流を-の流れと逆向きの+の流れととらえ直し、+の流れの向きを電流の向きと呼ぶ。
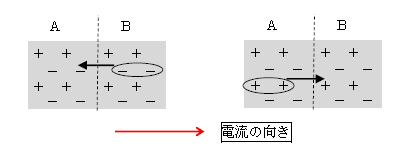
Aがー2個過剰、Bが+2個過剰になる結果に変わりはない
電流の大きさ(あるいは単に電流)の定義は
電流 \(I\)= 注目(している)断面を1sあたり通過する電気量 [C/s=A](アンペア)
例えば電流3Aとは、断面を1sあたり3C通過するという意味。
注目断面を微小時間\(\Delta t\)の間に通過する電気量が\(\Delta q\)なら(図5)
電流\(\displaystyle I=\frac{\Delta q}{\Delta t} \)
つまり、電流\(I\)×時間\(\Delta t\)=電気量\(\Delta q\)
[A × s =C/s×s=C] となる。
[ さらに\(\Delta t→0\)とすれば、
\(\displaystyle I=\lim_{\Delta t \rightarrow 0} \frac{\Delta q}{\Delta t}=\frac{dq}{dt} \)
微分についての説明は1-01-1を参照のこと。 ]