2-07-1: 定常波 ＜動画あり＞
重ね合わせの原理で生じる現象の第１弾 ―― 形の等しい２つの波が\(+V,-V\)で「定常波」 → ＜例題＞は2-07-2へ
※ ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 定常波 形 （振幅・波長）の等しい２つの波が速度\(+V,-V\)で重なり合うときの合成波。
波形は上下に振動するだけで、左右に移動しない。
節と節（腹と腹）の間隔は\(\frac{1}{2} \)波長。
・ 固定端は節、自由端は腹
これから2-07から2-12まで、重ね合わせの原理に基づいて起こる現象を考えていく。その第１が定常波 ―― 図１で話を始める。右に進む波(実線)、左に進む波(点線)、それらの合成波(赤線)が、\(t=0,\frac{T}{4}, \frac{T}{2}, \frac{3}{4} T \)（\(T\)は１周期）の４つの時刻で描かれている。右に進む波の山には○、左に進む波の山には□の目印が付けてある。2-01-1でやった通り、波は１周期で１波長進むから、\(\frac{T}{4}\)ごとに\(\frac{1}{4}\)波長、つまり\(x\)軸の２めもり分ずつ進む。○は右に２めもりずつ、□は左に２めもりずつ。
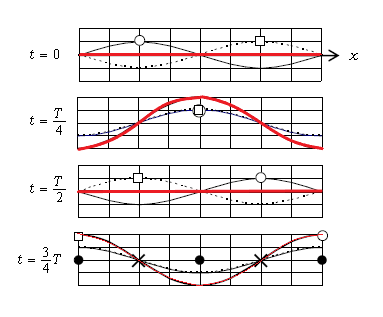
まず\(t=0\)では、実線と点線の\(y\)方向の変位が\(x\)軸上どの位置でも絶対値が等しく逆符号だから、重ね合わせの原理により、合成波(赤線)の変位は\(x\)軸上いたる所0である。
次に\(t=\frac{T}{4} \)では、実線と点線の変位がいたる所等しいから、合成波の変位は実線・点線の２倍である。
ここは大事な所。図１のグラフを「自分の手で」実際に写しながら、波の動きを理解しよう。
\(t=\frac{T}{2}, \frac{3}{4} T \)も同様に見て行くと、時間が\(t=0～\frac{3}{4} T \)と経過しても✕の場所は合成波(赤線)が全く上下に振動しない不動点、一方●の場所は最大振幅で上下に振動する点であることが分かる。✕を 節 、●を 腹 という。
面白いことに、不動点✕があるため、\(t=0～\frac{3}{4} T \)と経っても合成波(赤線)は左右に移動して見えない。振幅・波長の等しい、つまり形の等しい２つの波が\(+V,-V\)の速度で重なり合うときの合成波は、上下に振動するだけで左右に移動しない。これを定常波という。グラフより節と節（腹と腹）の間隔は\(\frac{1}{2}\)波長である ―― 重要。
ここで是非動画を見てみよう。
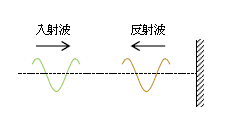
定常波は、例えば入射波と反射波が重なり合うときに生じる（図２）。2-06-1の通り固定端は振動できないから 節 になる一方で、自由端は自由に振動できて結論だけ記すと 腹 になる。
