2-06-1: 波の反射
反射波形の作図の練習題も含んでいます!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 自由端 反射端にて
反射波の変位=入射波の変位
固定端 反射端にて 反射波の変位=\((-1)\)×入射波の変位
・ 反射波形の描き方
自由端: 入射波形を壁越しに書き連ねたものをそのまま折り返す
固定端: 入射波形を壁越しに書き連ねたものを、上下逆さまにしてから折り返す
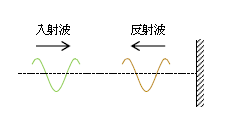
この単元では、ひもを伝わる波を例にとって波の反射を説明していく。図1のように壁(反射端という)があって、その左側にひもがピンと張ってあるとする(点線)。壁に向かって進む波を入射波、壁から離れていく波を反射波という。入射波も反射波も、1点のひもの粒子の振動が少し遅れたタイミングで隣りの粒子の振動を引き起こしながら、波形が平行移動していく。2-01-1で触れたように、波形が平行移動していく原因は媒質粒子どうしの間に働く張力だ。
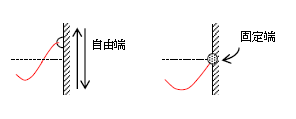
2種類の反射端を押さえよう(図2)。第1は、なめらかなカーテンレールを壁沿いに鉛直にくっ付けて、カーテンを取付けるはずのレールの輪にひもを取付けたなら、ひもは輪(反射端)とともにレールに沿って自由に振動できる。これを自由端という。第2は、ひもを壁に固定したなら、ひもは壁(反射端)に沿って振動できない。これを固定端という。
自由端では、反射端にて 反射波の変位(高さ)=入射波の変位 (1)
こうなる理由は ―― 入射波によって輪が振動している任意の時刻を考える。ひもは壁の右側にはないので右に振動を伝えることができず、代わりに左へ振動を伝えようとする。反射波が発生するのである。このとき、自由端は「自由」であるがゆえに、反射波に対して何ら特別な効果を及ぼさず、(1)のようになる。(*) [ 自由端の正確な定義は、振動の方向に力を及ぼさない反射端である。参考までに、この「力を及ぼさない」ことを大学レベルの数式で突き詰めていくと、(*)のような言葉の説明ではなく、数学的に(1)を証明できる。]
なお、(1)が成り立つのはあくまでも反射端(壁際)であって、それ以外の場所(壁際以外)では言えない。ともかくも反射端では(1)が成り立つから、図3(a)のように、入射波の振動(緑)と同じ高さを保ちつつ反射波が振動し(黄色)、それを波源として反射波が伝わる。
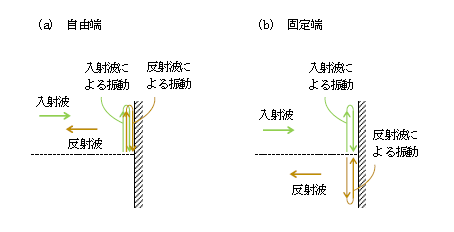
一方、固定端では、反射端にて 反射波の変位(高さ)=\((-1)\)×入射波の変位 (2)
この理由は ―― 2-05-1の重ね合わせの原理によれば、反射波の変位+入射波の変位=合成波の変位で、合成波のみが観測される。ところが図2のすぐ上に記した通り、固定端は振動できないから、反射端にて観測される合成波の変位(高さ)が恒等的に0。つまり、反射波の変位+入射波の変位=0 で(2)が言える。
図3(b)のように、入射波の振動(緑)と逆の高さを保ちつつ反射波が振動し(黄色)、それを波源として反射波が伝わる。
(1)(2)より、反射波形の描き方は次のようになる。[ 以下の描き方の説明は「波の式」なるものを用いて明確に数学的に裏付けることができる。興味のある人は単元2-06-2を参考にしてほしい。] 図4で\(y\)軸上に壁(灰色)があるものとする。
自由端: 入射波形(図4上の段の緑)を壁越しに書き連ねたもの(緑の点線)をそのまま折り返す(左向きの黒矢印)。橙が反射波形である。こうする理由は、壁の右側にはひもがないから反射波形を壁の左側に書くのであるが、(1)の段落で述べた通り自由端は反射波に対して特別な効果を及ぼさないから、壁越し(右側)にひもがあったならできるであろう入射波形を、そのまま折り返して書けば反射波形になるということ。なお、これは\(y\)-\(x\)グラフで、ある一瞬の波形を表している。右へ行くほど時間\(t\)が経過しているという意味はないので、念のため。図4を見ると、確かに反射端で(1)が成り立っている(図4の瞬間に限らず任意の瞬間に、この段落冒頭の黄色いマーカーを付けた方法で\(y\)-\(x\)グラフを書いたとしてもだ)。赤は入射波と反射波の合成波で、いま入射波と反射波の高さが横軸のどの位置でも等しいから、合成波は入射・反射波の2倍の高さになっている。
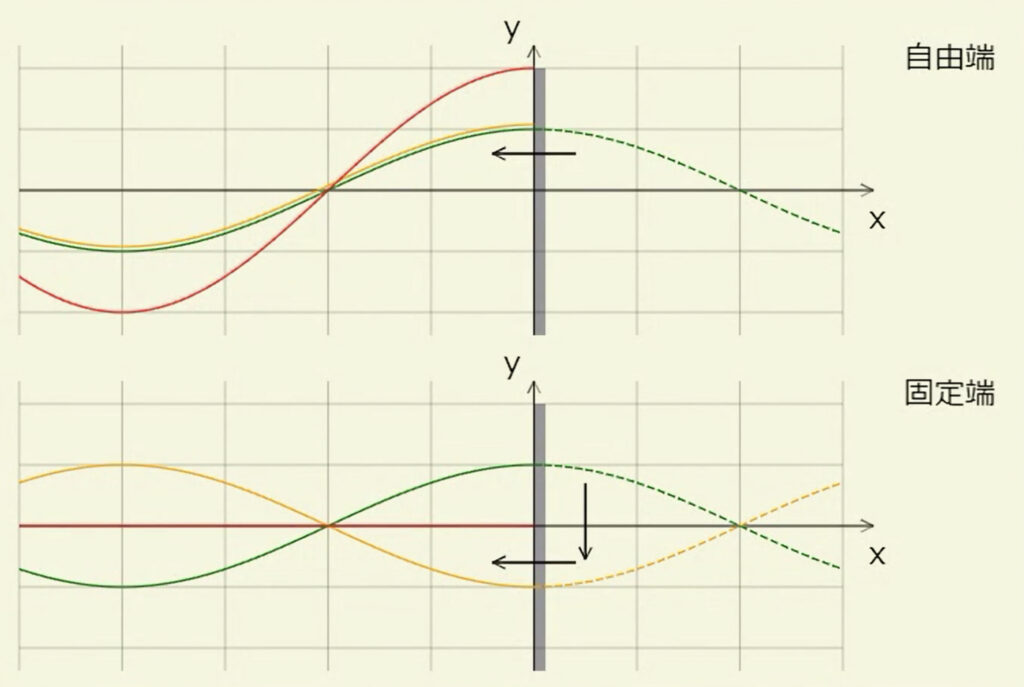
固定端: 入射波形(図4下の段の緑)を壁越しに書き連ねたもの(緑の点線)を、上下逆さまにしてから(下向きの黒矢印、橙の点線)折り返す(左向きの黒矢印)。橙の実線が反射波形。上下逆さまの操作を入れてやることで、(2)が成り立っている(図4の瞬間に限らず任意の瞬間に、この段落冒頭の黄色いマーカーを付けた方法で\(y\)-\(x\)グラフを書いたとしてもだ)。赤は入射波と反射波の合成波で、いま入射波と反射波の高さが横軸のどの位置でも互いに(-1)倍になっているから、合成波の高さはいたる所0である。
ここで、反射波形の例をもう1つ挙げておこう(図5)。緑の実線が入射波形。上の段の自由端は、緑の点線を折り返した橙が反射波形。下の段の固定端は、緑の点線を上下逆さまの橙の点線とし、それを折り返した橙の実線が反射波形。
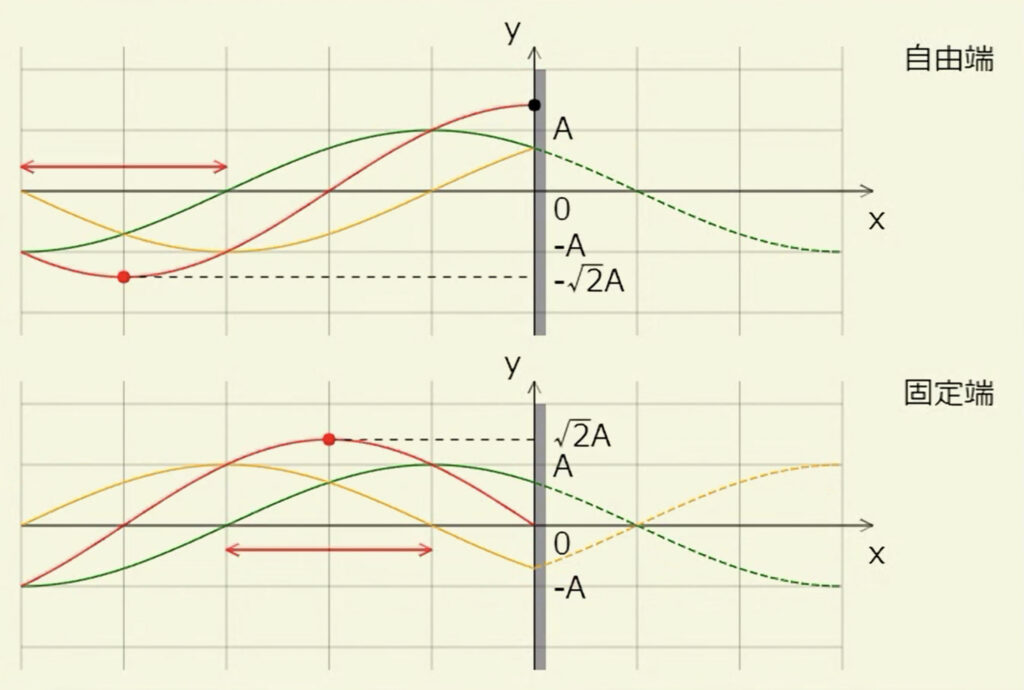
下の段で赤丸を付けた合成波の高さが、入射波の振幅\(A\)の\(\sqrt{2}\)倍である理由は ―― 赤い両方向矢印の範囲は緑にせよ橙にせよ\(\frac{1}{4}\)波長分で、サインカーブの\(\sin\)0°から\(\sin\)90°に相当。両方向矢印の中点の赤丸の高さは、
入射波(緑)\(\sin\)45°+反射波(橙)\(\sin\)45°\(=\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}=\sqrt{2}\)倍
になっているということ。上の段の赤丸の高さが\(-\sqrt{2}A\)である理由も同様で、してみると黒丸の高さは\(\sqrt{2}A\)である。
図4は\(\frac{1}{4}\)波長ごと、図5は\(\frac{1}{8}\)波長ごとの目盛りを横軸に入れて、「自分の手で」実際に、入射波形から反射波形及び合成波形を作図する練習題をやってみると勉強になる。


