1-36-1: 見かけの重力 <例題>
見かけの重力という入試で頻出の考え方をしっかりマスターしましょう! → 慣性力 の説明は1-35-1へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 重力\(mg\)と慣性力との合力を\(mg’\)と表し、
\(mg’\)を見かけの重力、\(g’\)を見かけの重力加速度という。
例題
図aのように、電車の天井から質量\(m\)のボールを長さ\(l\)の糸でつるした。 糸の質量と太さは無視できるものとし、かつ、糸は伸び縮みしないものとする。いま、電車の中で静止している人Aと電車の外で静止している人Bがボールを観察する。ボールは電車に比べて質量が十分小さく、ボールの運動は電車の運動に影響を与えないものとする。電車を水平方向右向きにに等加速度直線運動させると、糸は鉛直方向と角度\(\phi\)で静止した。電車の床からボールまでの高さを\(h\)、重力加速度を\(g\)とし、空気抵抗とボールの大きさは無視できるものとする。
問1 観測者A、Bそれぞれから見たとき、ボールにはどのような力がはたらいているように見えるか。ボールにはたらいている力の方向を矢印で描き、かつ、力の名称を書け。
問2 電車の加速度の大きさを\(\phi\)と\(g\)を使って表せ。
問3 ボールを電車の進行方向に単振り子のようにわずかに揺らしたとき、観測者Aからみた振り子の周期を求めよ。
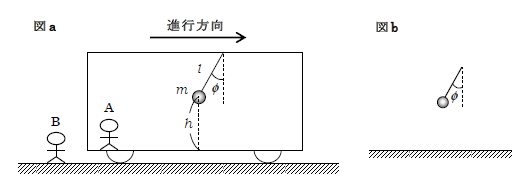
ボールを揺らさずに、ハサミで糸を切り落下させた。その後、ボールは床に完全弾性衝突した。
問4 観測者A、Bそれぞれから見たとき、糸を切ってからボールが床に衝突し最高点に達する前まで程度の軌跡の概略を図bに書け。ただし、この間ボールは電車内部の壁や観測者A、Bにぶつからないものとする。
問5 観測者Aから見たとき、問4で糸を切ってから床に衝突するまでにボールが水平方向に進んだ距離\(x_1\)と、床に衝突してから再び高さ\(h\)の位置に来るまでにボールが水平方向に進んだ距離\(x_2\)の比を求めよ。
解答・解説
問1 (電車とともに)加速度運動する観測者Aからは、慣性力が働いて見える。1-35-1の通り、慣性力の向きは観測者(電車)の加速度の向き右向きと逆向きの左向き。一方、大地上に静止している観測者Bからは慣性力は働いて見えない。よって 答は図1のようになる。
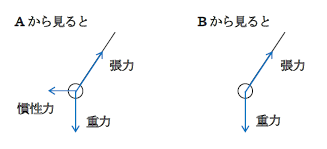
問2 問題文に「糸は鉛直方向と角度\(\phi\)で静止」とあるから、電車に乗っているAから見てつり合いの式が立てられる。1-05-1の通り、つり合いとは合力が0になることだから、図1の「Aから見ると」の図中の3本の力の合力(ベクトル和)が\(\vec{0}\)になる作図をすればよく、それが図2。3本のベクトルの足し算が\(\vec{0}\)だから、直角三角形が閉じる。
ここで、1-35-1の通り慣性力の大きさは、加速度座標系(加速度運動する観測者A)の加速度つまり電車の加速度\(a\)として\(ma\)である。図2より \(ma=mg\tan\phi\)
∴ \(a=\) 答 \(g\tan\phi\)
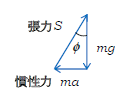
問3 Aから見ると重力\(mg\)と慣性力\(ma\)の合力は、質量\(m\)に比例する力であるという意味において1本の力\(mg’\)のように書ける(図3)。\(mg’\)を「見かけの重力」、\(g’\)を「見かけの重力加速度」という。重力\(mg\)と慣性力\(ma\)の2本で考えるよりも、1本にまとめて見かけの重力\(mg’\)だけとする方がラクだ、という発想である。図3より \(\displaystyle mg’=\frac{mg}{\cos\phi}\)
∴ \(\displaystyle g’=\frac{g}{\cos\phi}\) (1)
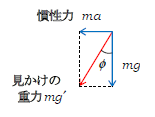
ボールがどの位置にあっても\(mg\)と\(ma\)は働いているから、どの位置でもみかけの重力\(mg’\)が働くことになる(図4)。通常の単振り子(1-23-2)は\(mg\)の働く鉛直方向の両側に振れる(図5)が、図4では見かけの重力\(mg’\)の働く角度\(\phi\)傾いた方向の両側に振れる。この鉛直方向から\(\phi\)傾いた直線を「見かけの鉛直線」という。電車とともに動くAから見た空間は、重力の方向(鉛直方向)が\(\phi\)傾いた特殊な空間と見なせるとも言える。
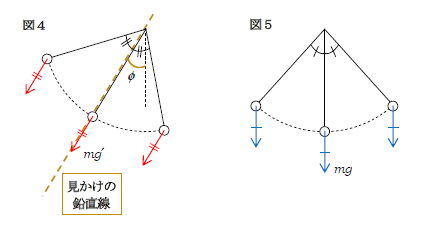
図4の見かけの鉛直線をあえて上下方向に書き直すと、1-23-2図1の\(mg\)を\(mg’\)に書き換えただけの図になることが分かる。よって1-23-2の単振り子の周期\(T=2\pi\sqrt{\frac{l}{g}} \) の代わりに\(g\)を\(g’\)と書き換えて
図4の振り子の周期\(\displaystyle T’=2\pi\sqrt{\frac{l}{g’}} \) (1)を代入して
\(T’=\) 答 \(\displaystyle 2\pi\sqrt{\frac{l\cos\phi}{g}} \)
問4 糸を切れば張力\(S\)は働かなくなる。Aから見ると、ボールは見かけの重力\(mg’\)だけを受けて見かけの鉛直線に沿って真っすぐ進む(図4)。これを称して、見かけの重力加速度\(g’\)の方向への「自由落下」と呼ぶことができる。ボールはやがて床へと達し、問題文の通り床と弾性衝突する。その直前・直後の図が図6。
さて、1-31-3の通り弾性衝突では運動エネルギーが保存するから、衝突前後で\(\frac{m}{2}v^2\)は不変、つまり\(v\)(赤)は不変。運動エネルギーが保存するということは摩擦熱が発生して運動エネルギーが失われることはない。すなわち床面に平行に摩擦力は働かない。「力が加わらないと物体は等速」(ニュートンの運動の第1法則)だから、床に平行な速度成分\(v_{//}\)(青)も不変。また1-30-1の最後の段落にある通り、弾性衝突ははね返り係数が1で、床(固定面)とボールが斜めに衝突するような場合は固定面に垂直な速度成分の大きさが不変だから\(v_⊥\)(緑)も不変。すると赤、青、緑の成す2つの直角三角形が合同になるから、入射角\(\phi\)=反射角となる。これを称して「固定面との弾性衝突では等角反射が起こる」という。
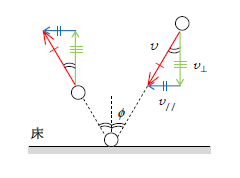
こうして等角反射して以後も、角度\(\phi\)傾いた見かけの重力\(mg’\)の下で運動するから、結局 答は図7のような軌跡
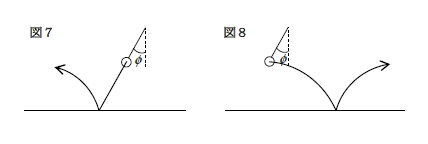
一方Bから見ると、ボールには通常の鉛直下向きの重力\(mg\)のみが働く(慣性力はない)から、通常の放物運動になる。 糸が切れる瞬間、Bから見てボールは電車と同じ右向きの速度で投げ出されるから、「水平投射」である。床との等角反射の後も通常の放物運動だから 答は 図8
問5 いつも通りの1-08-1: 力学攻略の基本 の流れに従って行こう(図9)。
まず軸と力 水平左向きに\(x\)軸、鉛直上向きに\(y\)軸を取る。Aから見て、力は図3と全く同様。
次に\(ma=F\) \(ma_x=ma=mg\tan\phi\) ∴ \(a_x=g\tan\phi\) ゆえに運動の水平成分は等加速度運動である。1-15-1の通り通常の放物運動の水平成分が等速であるのに比して、いまは慣性力\(ma\)が働くために等加速度である。
\(ma_y=-mg\) ∴ \(a_y=-g\) ゆえに運動の鉛直成分は重力加速度\(g\)による通常の落下運動である。図6の通り、床(固定面)との衝突直前直後で速度の鉛直成分(固定面と垂直な成分)の大きさは変わらない。ここで1-15-3の等加速度運動の対称性(等加速度直線運動の折返し点までの距離が等しい地点に関して、折り返し点までにかかる時間と折返し点からかかる時間は等しい)を思い出そう。すると、糸を切ってから衝突するまでの時間を\(t_1\)とすれば、衝突してから高さ\(h\)に戻るまでの時間もまた\(t_1\)であると言える(図9 あくまでも運動の鉛直成分に着目しよう)。
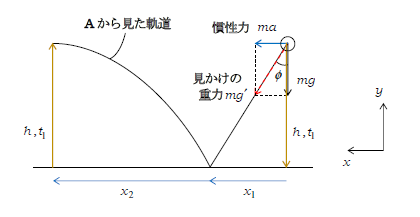
運動\(v,x\)を調べる 図9で等加速度の公式\(x=x_0+v_0 t+\frac{1}{2}at^2 \)より
\(\displaystyle x_1=\frac{1}{2}a_xt_1^2\) かつ \(\displaystyle x_1+x_2=\frac{1}{2}a_x(t_1+t_1)^2\)
∴ \(x_1:(x_1+x_2)=t_1^2:4t_1^2=1:4\)
∴ \(x_1:x_2=\) 答 \(1:3\)


