1-16-1: 運動エネルギーと仕事

「運動エネルギー」「仕事」という重要な概念をきっちり理解しましょう！　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

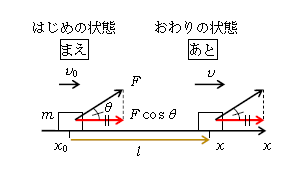
　質量\(m\)の物体に力\(F\)を加え続けて距離\(l\)動かす状況を考える（図１）。\(F\)が斜め上向きなのは、例えば人が肩にひもをかけて引張っているイメージ。「力\(F\)のうち物体の移動方向(\(x\)方向)に平行な成分」\(F\cos\theta \)を、略して「力の移動方向成分」と呼ぼう。ここでは、\(F\cos\theta \)が一定の場合を考える。
　まずは定義から。（1-02-1でやった通り、「○○と呼ぶ・名付ける・決める」タイプの式を定義式という。名付けておくと役に立つから定義するわけである。）
　運動エネルギー\(=\)\(\displaystyle \frac{m}{2} v^2\)　（\(\displaystyle \frac{m}{2} v^2\)を運動エネルギーと呼ぶ）
　仕事\(W=\)(力の移動方向成分)×(距離) \(=F\cos\theta ×l \)（とりあえず日常用語の「仕事」のことは忘れて、物理用語としての「仕事」と呼ばれるもの、くらいに思っておこう。）
　また、運動エネルギー変化＝ (あとの運エネ) － (まえの運エネ)　（図１）
　　　　　　　　　　　　　＝　　\(\displaystyle \frac{m}{2} v^2 \)    　 －　　 \(\displaystyle \frac{m}{2} v_0^2\)
と定義する。このように定義すると、

　運動エネルギー変化＝仕事　　つまり、　　　
　　\(\displaystyle \frac{m}{2} v^2 -\frac{m}{2} {v_0}^2=W \:\, \)　　　　　　　　 (1)
が成り立つことが以下のように証明できる。

　　証明　等加速度の公式
　　　　\(v=v_0+at \)　　　　　　　　　　　(2)
　　　　\(x=x_0+v_0t+\frac{1}{2}at^2 \, \)　　　　　　(3)　　を用いる。
　　　いま（後々うまく行くので）\(v^2-{v_0}^2\)を計算してみると　
　　　　\(=(v+v_0)(v-v_0) \)
　　　(2)を代入　\(=(2v_0+at)at \)\(=2(v_0+ \frac{1}{2} at)at \)
　　　　\(=2a(v_0+ \frac{1}{2} at)t \)\(=2a(v_0 t+ \frac{1}{2} at^2) \)
　　　(3)を代入　\(=2a(x-x_0) \)
　　　ここで両辺を\(\frac{m}{2} \)倍する
　　　　\(\displaystyle \frac{m}{2} v^2 -\frac{m}{2} {v_0}^2 =ma(x-x_0) \)　　(4)
　　　図１で\(x\)方向の運動方程式 \(ma=F\cos\theta \) 及び
　　　\(x-x_0=l\) を(4)の右辺に代入
　　　　\(\displaystyle \frac{m}{2} v^2 -\frac{m}{2} {v_0}^2=F\cos\theta ×l=W \)
　　　よって(1)が証明された

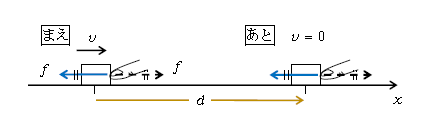
　ところで、運動エネルギーとは結局何なのか。それを理解するために、運動エネルギー\(\frac{m}{2} v^2 \)を持つ物体を、運動の向きと逆向きに手で一定の力\(f\)を加えながら手を後ろに引きつつ、物体を静止させてみる（図２）。
　このとき、手が物体にした仕事（手から物体に働く左向きの\(f\)のした仕事）は
　　\(W=\)(力の移動方向成分)×(距離) \(=-f×d\)
　つまり、力の向きと移動の向きが逆ならば、力の移動方向成分が負になるから仕事は負だ。すると(1)より　
　　あと\(-\)まえ\(\displaystyle =\frac{m}{2} 0^2 – \frac{m}{2} v^2=-fd \)　　
　　∴　\(\displaystyle fd=\frac{m}{2} v^2 \)　　　　　　　　　　　　(5)　

　一方、作用反作用により、物体が手にした仕事（物体から手に働く右向きの\(f\)のした仕事）は
　　\(W’=+f×d\)　
　(5)を代入して　\(\displaystyle W’=\frac{m}{2} v^2 \)
　ということは、「運動エネルギー\(\frac{m}{2} v^2 \)の物体は、静止するまでに他の物体(手)に\(W’=\frac{m}{2} v^2 \)だけ仕事をすることができる」ということになる。この「他の物体にすることができる仕事の量」「仕事する能力」のことをエネルギーと呼んでいる。1-17-1ではまた別のエネルギー「位置エネルギー」が登場する。
　こうして結局(1)の意味は、「物体はされた仕事の分だけ仕事する能力（運動エネルギー）を増やす」となる。
　なお、力の向きと移動の向きが垂直の場合、図１で\(\theta=90°\)となって \(W=F\cos90° ×l =0\)、すなわち仕事は０である。[ 力の向きと移動の向き(右向き)が垂直だと、図１のような場合では物体を右向きに距離\(l \)移動させることはできない。が、力が何本か加わりつつ物体が右向きに移動し、ある特定の１本の力（例えば垂直抗力）が移動の向きと垂直であるような場合、その力のする仕事は０になる。このような状況が今後よく出てくる。]

　単位について確認しておこう。
　仕事\(W=F\cos\theta ×l \)で、\(F\)の単位は1-05-1の通り[N=\(\text{kg} \cdot \)m/s\(^2\)]、\(\cos\theta \)は単なる数で単位なし、\(l\)の単位は[m]だから、仕事\(W\)の単位は[N\(\cdot \)m=(\(\text{kg} \cdot \)m/s\(^2\))\(\cdot \)m=\(\text{kg} \cdot \)m\(^2\)/s\(^2\)]。これを[ J ]（ジュール）という。
　運動エネルギー\(\frac{m}{2} v^2 \) の単位は［\(\text{kg} \cdot \)(m/s)\(^2 \cdot \)m=\(\text{kg} \cdot \)m\(^2\)/s\(^2\)=J］
　運動エネルギーの単位も仕事の単位も[J]で等しいのは、(1)より運動エネルギー変化=仕事だから当然である。
　[ なお、仕事について発展的な学習をしたい人は、10-02-1を参照するとよい。 ]