10-02-1: 力には向きがある、仕事には向きがない #その1
物理を習ったことのある人なら誰もが抱く疑問を明快に解き明かします! 中・上級者向きの内容です。 → <#その2>は10-02-2へ、<#その3>は10-02-3へ
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
物理では力には向きがあって力はベクトル量だと言う。例えば正の向きを向いた力は+5Nといい、負の向きを向いた力は\(-\)3Nという。
一方物理では、力に移動距離をかけたものを仕事と言う。力の向きと移動の向きが同じであれば正の仕事、例えば+20Jといい、逆であれば負の仕事、\(-\)16Jという。このように仕事は正負の符号を持つ。しかし仕事は向きのあるベクトル量ではなく、向きのないスカラー量だと言う。仕事には符号はあるが、向きはないということらしい。これは一体どういうことなのだろう。そもそも「向きがある」とは物理的にはどういう意味なのだろう。ベクトル、スカラーを物理ではどのように捉えているのだろうか。
簡単な準備から始めよう(図1)。傾角\(\theta\)の斜面の下端から、質量\(m\)の小球を斜面に対する角度\(\phi\)、初速度\(v_0\)で投げ出したとき、小球が再び斜面に落下するまでの時間を計算してみる。
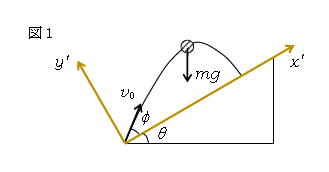
解法の1つとしては、斜面に平行な方向、垂直な方向をそれぞれ\(x’\)軸、\(y’\)軸に取り、重力\(mg\)を\(x’\)成分\(-mg\sin\theta \)、\(y’\)成分\(-mg\cos\theta \)に分解する。運動方程式の
\begin{equation} \tag{I} \begin{cases}
x’成分 & m{a_x}’=-mg\sin\theta \\
y’成分 & m{a_y}’=-mg\cos\theta
\end{cases} \end{equation} ∴ \({a_y}’=-g\cos\theta \)
斜面に落下するとき\(y’=0\)となるから、求める時間\(t\)は
\(y’=0=v_0\sin\phi \cdot t -\frac{1}{2} g\cos\theta \cdot t^2 \)\(\displaystyle ∴ t=\frac{2v_0\sin\phi}{g\cos\theta} \tag{1} \)
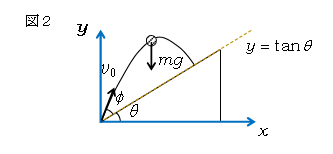
いま1つの解法としては、水平方向、鉛直方向にそれぞれ\(x\)軸、\(y\)軸を取り(図2)、運動方程式の
\begin{equation} \tag{II} \begin{cases}
x成分 & ma_x=0 \\
y成分 & m{a_y}’=-mg
\end{cases} \end{equation} ∴ \(a_x=0, a_y=-g\)
∴ \(x=v_0\cos (\theta +\phi) \cdot t \)
\(y=v_0\sin (\theta+\phi) \cdot t -\frac{1}{2} gt^2 \)
斜面に落下するとき\(y=\tan\theta \)となるから、
\(v_0\sin (\theta+\phi) \cdot t -\frac{1}{2} gt^2=v_0\cos (\theta +\phi) \cdot t \cdot \tan\theta\)\(\displaystyle ∴ t=\frac{2v_0\text{{} \sin(\theta+\phi)-\cos(\theta+\phi)\tan\theta \text{}} }{g} \tag{2} \)
答の(1)と(2)は一見すると違うように見えるが、
(2)の{ }の中身=\(\displaystyle \sin(\theta+\phi) -\cos(\theta+\phi) \frac{\sin\theta}{\cos\theta} \)
\(\displaystyle =\frac{\sin(\theta+\phi)\cos\theta -\cos(\theta+\phi)\sin\theta}{\cos\theta} \)
[加法定理により] \(\displaystyle =\frac{\sin(\,(\theta+\phi)-\theta\,)}{\cos\theta} =\frac{\sin\phi}{\cos\theta} \)
となるので、(1)と(2)は一致する。つまり\(x’\)-\(y’\),\(x\)-\(y\)どちらの座標軸で現象を記述しても、得られる結論は同じになる。
一方次のことも判明した。座標軸が\(x’\)-\(y’\)であるときには運動方程式は(I)のようになり、\(x\)-\(y\)のときには(II)のようになる。つまり座標軸の取り方によって、法則の数式的表現が全く別物になってしまうということである。これは心地悪くないだろうか。そもそも小球が飛ぶというような物理現象は、人間が座標軸を取ろうと取るまいとそんなことにはお構いなく営まれていて、状況設定が同じならばいつも同じように起こる、同じ結論をたどる、つまり一定の規則性 ―― 法則性 ―― があるのである。その物理法則性の数式的表現が、人間側の座標軸の取り方次第で幾通りにも変わってしまうというのでは、何とも不便ではないか。
ところが運動方程式をベクトル式で書いてみよう。すると\(m\vec{a}=m\vec{g} \tag{III}\) このベクトル式の意味するところは、座標軸をどう取ろうとも、ともかく起こることは「重力\(m\vec{g} \)が加われば、それと同じ向きに加速度\(\vec{a}=\vec{g} \)が生じる、その加速度\(\vec{g} \)に従って小球は運動する」ということである。たまたま座標軸\(x’\)-\(y’\)を取れば \(m\vec{g} \)の成分は \( (-mg\sin\theta, \, -mg\cos\theta ) \)になるし、座標軸\(x\)-\(y\)を取れば\( (0, \, -mg) \)になる、しかし「重力によって加速度が生じる」といった意味内容の現象が起こることには全く変わりがない(現に(1)と(2)の答は一致した)。であるならば、座標軸の取り方に全く影響されることのない、「力が加われば加速度が生じる」ことの数式的表現があって然るべきではないか、それがベクトル式(III)である。


