3-03-2: 電場と電位 <例題1>
この例題1と3-03-3の例題2を解けば、電場と電位の理解が格段に深まること請け合いです! → 関連単元は3-02-1電場と電気力線、3-04-1等電位線 ; 電場と電位差の関係
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 合成電場はベクトル和を取る(\(x\)成分,\(y\)成分別々に和を取ることができる)。
合成電位は単純な和を取る。
例題
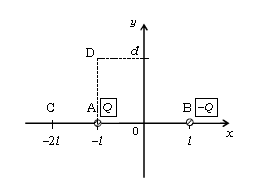
図のように\(x\)軸上の点A(\(-l,0\)), 点B(\(l,0\))(ただし\(l>0\))に電気量がそれぞれ\(Q\) ,\(-Q\)(ただし\(Q>0\))の二つの点電荷を固定した。クーロンの法則の比例定数を\(k\)とし、無限遠の点を電位の基準点とする。
問1 点C(\(-2l,0\))における電場の\(x\)成分\(E_x\)と電場の\(y\)成分\(E_y\)を求めよ。
問2 点Cにおける電位\(\phi\)を求めよ。
問3 点D(\(-l,d\))(ただし\(d>0\))における電場の\(x\)成分\(E’_x\)と電場の\(y\)成分\(E’_y\)を求めよ。
問4 点Dにおける電位\(\phi’\)を求めよ。
解答・解説
問1 3-02-1の通り、電場とは1Cあたりに働く力[N/C]である。ゆえに点Cでの電場\(\vec{E}\)を知りたければ(図1)、点Aの電荷\(+Q\)が点Cの+1Cに及ぼす力、すなわち電場\(\vec{E_A}\)(その向きは\(+Q\)から+1Cへの斥力の向き)を求め、次いで点Bの電荷\(-Q\)が+1Cに及ぼす力\(\vec{E_B}\)(\(-Q\)から+1Cへの引力の向き)を求め、それらを合成すればよい(ベクトル和を取ればよい):合成電場\(\vec{E}=\vec{E_A}+\vec{E_B}\)
電場の大きさ\(E_A\)は3-02-1の通り距離\(\overline{AC}\)の2乗に反比例するから、
\(\displaystyle E_A=k\frac{Q}{\overline{AC}^2}=\frac{kQ}{l^2}\)
同様に\(\displaystyle E_B=k\frac{Q}{\overline{BC}^2}=\frac{kQ}{(3l)^2}=\frac{1}{9}\frac{kQ}{l^2}\)
ベクトル和の計算は\(x\)成分,\(y\)成分別々に調べていくのが基本。
\(x\)成分\(\displaystyle E_x=-E_A+E_B=\) 答 \(\displaystyle -\frac{8}{9}\frac{kQ}{l^2}\)
\(y\)成分\(E_y=\) 答 \(0\)
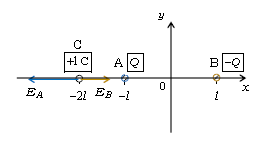
問2 3-03-1の通り、電位とは1Cあたりの持つ(電気力による)位置エネルギー[J/C=V]である。ゆえに点Cでの電位\(\phi\)を知りたければ、点Aの電荷\(+Q\)が点Cの+1Cに持たせる位置エネルギー、すなわち電位\(\phi_A\)を求め、次いで点Bの電荷\(-Q\)が+1Cに持たせる位置エネルギー\(\phi_B\)を求め、それらを足せばよい:合成電位\(\phi=\phi_A+\phi_B\)
ここで電位とは要は「エネルギー的な高さ」(3-03-1)のことであるから、電荷\(+Q\)のつくるエネルギー的な高さ\(\phi_A\)と、電荷\(-Q\)のつくるエネルギー的な高さ\(\phi_B\)とを、単純に足す。この単純な和のことを「スカラー和」ともいう。ベクトル和を取る電場と、単純な和を取る電位との違いにくれぐれも注意しよう。ちなみに、エネルギーは向きと大きさを持つベクトルではない(その詳しい説明に興味のある者は1-16-3を参照のこと)。ゆえに電位(1Cあたりの持つ位置エネルギー)もベクトルではない。ベクトルの電場は矢印で図示できたが(図1)、ベクトルでない電位は矢印で図示することはできない。
3-03-1の通り、電位は距離\(\overline{AC}\)の1乗に反比例するから、
\(\displaystyle \phi_A=k\frac{Q}{\overline{AC}}=\frac{kQ}{l}\)
同様に\(\displaystyle \phi_B=k\frac{-Q}{\overline{BC}}=k\frac{-Q}{3l}\) [ 負電荷\(-Q\)のつくる電位は負である(3-03-1) ]
よって \(\displaystyle \phi=\phi_A+\phi_B=\) 答 \(\displaystyle \frac{2}{3}\frac{kQ}{l}\)
問3 (図2)問1と同様に合成電場\(\vec{E’}=\vec{E’_A}+\vec{E’_B}\)
いま、大きさ\(\displaystyle E’_A=k\frac{Q}{\overline{AD}^2}=\frac{kQ}{d^2}\)
\(\displaystyle E’_B=k\frac{Q}{\overline{BD}^2}=\frac{kQ}{(2l)^2+d^2}=\frac{kQ}{4l^2+d^2}\) [ △DABでの三平方の定理を用いた ]
また、図の\(\theta\)について \(\displaystyle \cos\theta=\frac{2l}{\overline{BD}}=\frac{2l}{\sqrt{4l^2+d^2}}\) , \(\displaystyle \sin\theta=\frac{d}{\overline{BD}}=\frac{d}{\sqrt{4l^2+d^2}}\)
よって\(x\)成分\(\displaystyle E’_x=E’_B\cos\theta=\frac{kQ}{4l^2+d^2}\frac{2l}{\sqrt{4l^2+d^2}}=\) 答 \(\displaystyle \frac{2kQl}{(4l^2+d^2)^{\frac{3}{2}}}\)
\(y\)成分\(\displaystyle E’_y=E’_A-E’_B\sin\theta=\frac{kQ}{d^2}-\frac{kQ}{4l^2+d^2}\frac{d}{\sqrt{4l^2+d^2}}\)
\(=\) 答 \(\displaystyle kQ\left(\frac{1}{d^2}-\frac{d}{(4l^2+d^2)^{\frac{3}{2}}}\right)\)

問4 問2と同様に合成電位\(\phi’=\phi’_A+\phi’_B\)
いま\(\displaystyle \phi’_A=k\frac{Q}{\overline{AD}}=\frac{kQ}{d}\) , \(\displaystyle \phi’_B=k\frac{-Q}{\overline{BD}}=\frac{-kQ}{\sqrt{4l^2+d^2}}\)
よって\(\displaystyle \phi’=\phi’_A+\phi’_B=\) 答 \(\displaystyle kQ\left(\frac{1}{d}-\frac{1}{ {\sqrt{4l^2+d^2}}}\right)\)
→ 関連単元は3-02-1電場と電気力線、3-04-1等電位線 ; 電場と電位差の関係


