1-43-1: 重心運動

２体問題を時間の関数として扱う際には欠かせない、重心運動というテーマを扱います。！ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

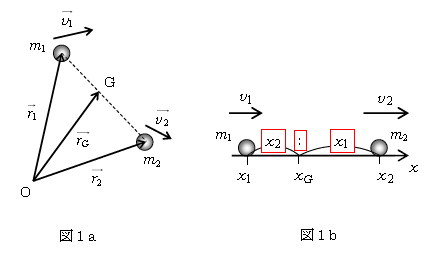
　まずは重心の定義から。以下で質点とは、その質量は考えるが大きさを無視する物体のことである（よく「小球」とも表現される）。質点1,2のそれぞれの質量が\(m_1,m_2\)、位置ベクトルが\(\vec{r_1},\vec{r_2}\)（始点をOとする）のとき、２質点の重心Gの位置ベクトル
　\(\displaystyle \vec{r_G}=\frac{m_1\vec{r_1}+m_2\vec{r_2}}{m_1+m_2}\)　
と定義する（図１a）。\(x\)軸上の２質点を考える場合は、質点1,2の\(x\)座標を\(x_1,x_2\)として、重心Gの\(x\)座標
　\(\displaystyle x_G=\frac{m_1x_1+m_2x_2}{m_1+m_2}\)
となる（図１b）。
　分母の\(m_1+m_2\)を\(m_2+m_1\)と書きかえて\(x_G=\frac{m_1x_1+m_2x_2}{m_2+m_1}\)と表せば、内分公式の形になっている。そう、重心Gとは、\(x_1,x_2\)を\(m_2:m_1\)に内分する点である（図１b）。\(x_1,x_2\)の添え字の順序1,2に対して、\(m_2,m_1\)の添え字の順序が2,1と逆転しているので、「\(x_1,x_2\)を質量の逆比に内分する点」とも表現する。これは、1-39-2で扱った「軽い棒＋小球２個」の重心と一致している。すなわち重心とは、2質点の全質量があたかも1点に集中しているかのように見なせる点である。

　次に重心速度\(\vec{v_G}\)は、速度\(\vec{v}\)の定義(1-16-2) \(\displaystyle \vec{v}=\lim_{\Delta t → 0} \frac{\Delta\vec{r}}{\Delta t}=\frac{d\vec{r}}{dt} \)により、
　\(\displaystyle \vec{v_G}=\frac{d\vec{r_G}}{dt}=\frac{d}{dt}\frac{m_1\vec{r_1}+m_2\vec{r_2}}{m_1+m_2}=\frac{m_1\frac{d\vec{r_1}}{dt}+m_2\frac{d\vec{r_2}}{dt}}{m_1+m_2}\)　
　ここで、定数\(m_1,m_2\)は微分せず、変数\(\vec{r_1},\vec{r_2}\)に微分記号\(\frac{d}{dt}\)を掛けた。質点1,2それぞれの速度\(\vec{v_1}=\frac{d\vec{r_1}}{dt}\), \(\vec{v_2}=\frac{d\vec{r_2}}{dt}\)として（図１aに\(\vec{v_1}\), \(\vec{v_2}\)を適当な向きに図示してある）、
　\(\displaystyle \vec{v_G}=\frac{m_1\vec{v_1}+m_2\vec{v_2}}{m_1+m_2}\)　となる。
　\(x\)軸上の２質点では、質点1,2の速度を\(v_1,v_2\)として（図１b）、
　重心速度\(\displaystyle v_G=\frac{m_1v_1+m_2v_2}{m_1+m_2}\)
　同様に、質点1,2の加速度\(\vec{a_1},\vec{a_2}\)として重心加速度\(\vec{a_G}\)は、加速度\(\vec{a}\)の定義(1-16-2) \(\displaystyle \vec{a}=\lim_{\Delta t → 0} \frac{\Delta\vec{v}}{\Delta t}=\frac{d\vec{v}}{dt} \)より、
　\(\displaystyle \vec{a_G}=\frac{d\vec{v_G}}{dt}=\frac{d}{dt}\frac{m_1\vec{v_1}+m_2\vec{v_2}}{m_1+m_2}=\frac{m_1\frac{d\vec{v_1}}{dt}+m_2\frac{d\vec{v_2}}{dt}}{m_1+m_2}=\frac{m_1\vec{a_1}+m_2\vec{a_2}}{m_1+m_2}\)　　(☆)
　\(x\)軸上では、質点1,2の加速度\(a_1,a_2\)として、
　重心加速度\(\displaystyle a_G=\frac{m_1a_1+m_2a_2}{m_1+m_2}\)

　では、いよいよ重心の運動方程式（あるいは重心運動の方程式）を考えることにしよう。まず、1-31-1で扱った「内力」「外力」のおさらいをしておこう。
　内力：２物体どうしで及ぼし合う作用反作用のペア
　外力：２物体以外から働く力
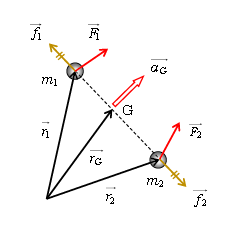
　ここで、図２のように質点1,2に加わる力を、それぞれ内力\(\vec{f_1},\vec{f_2}\)と外力\(\vec{F_1},\vec{F_2}\)に分類しておく（向きは適当に付けてある）。すると、質点1,2の運動方程式は
　1: \(m_1\vec{a_1}=\vec{f_1}+\vec{F_1}\)　　　　　　　　　　　　　　　　　 (1)
　2: \(m_2\vec{a_2}=\vec{f_2}+\vec{F_2}\)　　　　　　　　　　　　　　　　 　(2)
ただし、内力は作用反作用のペアで、\(\vec{f_1}\)と\(\vec{f_2}\)は互いに逆向き・等大だから、\(\vec{f_1}=-\vec{f_2}\)すなわち\(\vec{f_1}+\vec{f_2}=0\) が成り立っている。(1)と(2)を加えると、
　\(m_1\vec{a_1}+m_2\vec{a_2}=\vec{f_1}+\vec{f_2}+\vec{F_1}+\vec{F_2}=\vec{F_1}+\vec{F_2}\)　　(3)
　左辺に\(m_1+m_2\)を掛けて割って、左辺\(\displaystyle =(m_1+m_2)\frac{m_1\vec{a_1}+m_2\vec{a_2}}{m_1+m_2}\)
　(☆)を代入して、左辺\(=(m_1+m_2)\vec{a_G}\)。

　さらに右辺の\(\vec{F_1}+\vec{F_2}=\vec{F_外}\)とおけば、(3)は
　\((m_1+m_2)\vec{a_G}=\vec{F_外}\)
　これを重心運動の方程式という。その意味するところは「重心は全質量\(m_1+m_2\)を担い、外力\(\vec{F_外}\)のみによって加速される(内力は無関係)」。具体例は1-44-1で見ていくことにしよう。