1-39-2: 剛体の重心

重心についてしっかり理解しておきましょう！ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

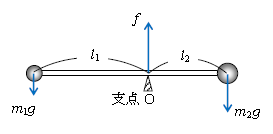
　1-39-1図３で扱った軽い棒＋小球２個を、図１に再掲した。1-39-1の通り、
　モーメントのつり合いは　\(0=m_1gl_1-m_2gl_2\)　　　　(1)
　力のつり合いは　　　　　\(0=f-m_1g-m_2g\:\,\)　　　(2)
　(1)より　\(m_1l_1=m_2l_2\)　　∴　\(l_1:l_2=m_2:m_1\)  　(3)
　(2)より　\(f=(m_1+m_2)g\)　　　　　　　　　　　　　(4)
　(3)では、 \(l_1,l_2\)の添え字の順序1,2に対して、\(m_2,m_1\)の添え字の順序が2,1と逆転している。これを、点Oは棒の長さを「質量の逆比に内分する」点であるという。

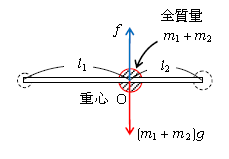
　(3)(4)から結論されるのは、「質量の逆比に内分する点Oに棒の全質量\(m_1+m_2\)が集中し、全重力\((m_1+m_2)g\)が集中し、それを下から支えると棒が静止する」かのように扱ってよいということ（図２）。この「全質量が１点に集中している かのように見なせる点」Oを重心と いう。軽い棒＋小球２個の重心は、質量の逆比に内分する点だ。

　質量の逆比に内分するということは、例えば\(m_1=1\text{kg},m_2=2\text{kg}\)と\(m_2\)の方が重ければ、\(l_1:l_2\)\(=m_2:m_1\)\(=2:1\)で\(l_2\)の方が小さい。重心は重い側に片寄る。重い側を支えるとつり合う。野球のバットも太い側を支えるとつり合う（うまくやればの話）。
　特に\(m_1=m_2\) のときは、\(m_2:m_1=1:1\) だから、重心は中心。これを少し応用すれば、
　密度が一様で線対称な剛体の重心は対称中心　　(☆)
であることが分かる。具体的には、一様な長方形の剛体の重心は対角線の交点、円板の重心は円の中心。
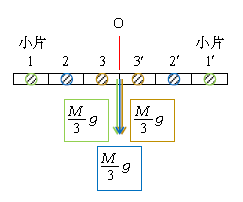
　(☆)の証明の概要だけを以下に示す。例として、太さの無視できる一様な棒の質量を\(M\)、中点をOとして、その重心がOであることを示そう（図３）。例えば棒を6等分して、左端から小片1,2,3、右端から小片1′,2′,3’と番号を振る。各小片の質量は\(\frac{M}{6}\)で、各小片の中点（図の〇印）に\(\frac{M}{6}\)ずつ集中していると見なす。まず小片1と1’を仮想的に軽い棒でつなぐと、その重心は質量の逆比\(\frac{M}{6}:\frac{M}{6}=1:1\)に内分する点Ｏ。つまり点Ｏに小片1と1’の全重力\((\frac{M}{6}+\frac{M}{6})g=\frac{M}{3}g\)（緑の矢印）が加わり、点Ｏを下から\(\frac{M}{3}g\)で支えるとつり合う。次に小片2と2’を軽い棒でつなぐと、重心は点Ｏ、そこにに\(\frac{M}{3}g\)(青の矢印)が加わる。最後に小片3と3’を軽い棒でつなぐと、重心は点Ｏ、そこに\(\frac{M}{3}g\)(黄色の矢印)が加わる。結局、棒全体を点Ｏで下から\(\frac{M}{3}g+\frac{M}{3}g+\frac{M}{3}g=Mg\)で支えるとつり合う。ということは、点Ｏに全質量\(M\)が集中していると見なせるので、点Oが重心である。

　証明をもう少し厳密にしたければ、棒を無限個等分し、左端から小片1,2,3,…、右端から小片1′,2′,3′,…と番号を振って同様の議論を繰り返せばよい。