1-31-1: 運動量保存則

力学的エネルギー保存則と並んで重要な運動量保存則を、１次元の衝突現象を題材にしっかりと身に付けましょう！　→　＜例題＞は1-31-2、1-31-3へ

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　図１のように\(x\)軸上を直線運動する２物体どうしが衝突する現象を１次元衝突という。衝突直前の速度\(v_2\)の物体B(質量\(m_2\))が、物体A(質量\(m_1\))から力\(F_2\)を受けて衝突直後に速度\(v’_2\)になり、直前\(v_1\)のAがBから\(F_2\)の反作用\(F_1\)を受けて直後に\(v’_1\)になる状況が示されている。

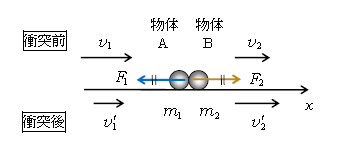
　その際、\(F\)-\(t\)グラフは典型的に図２のようになる。\(F_2\)で説明すると、力はあっという間に\(F_\text{max} \)になり（野球のバットでボールを叩いた瞬間写真でボールがグニャッと変形するあの瞬間だ）、あっという間に0 Nになり、力の加わっている時間\(\Delta t \)はひじょうに短い。\(F_1\)は作用反作用の法則により\(F_2\)の逆符号だから、\(F_2\)と上下対称のグラフになる。

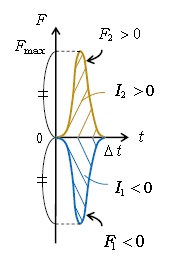
　力積\(I\)は1-28-1でやった通り、力が一定のときは力\(F\)×時間\(t\)、力が一定でないときは\(F\)-\(t\)グラフの面積。ゆえに物体Bの受ける力積\(I_2\)は図２の黄色い斜線部の面積で、物体Aの受ける力積\(I_1\)は青い面積。\(F_1<0\)だから\(I_1<0\)、すなわち横軸の下側の面積は負の値として扱う。
　さっそく運動量と力積の関係を立式していこう。すなわち
　　　　　　 あと\(-\)まえ
　運動量変化 \(mv-mv_0\)　=　力積\(I\)　　(＊)　　　
　図１でAに注目（Bをあえて見ない）: \(m_1v’_1-m_1v_1=I_1　<0 \)　　(1)
　図１でBに注目（Aをあえて見ない）: \(m_2v’_2-m_2v_2=I_2　>0 \)　　(2)　
　(＊)の意味は「力積の分だけ運動量が変化する」。(1)の力積\(I_1\)は負で、例えば\(I_1=-5\)のような値だから、力積\(-5\)の分、運動量が\(-5\)変化する、つまり運動量が\(5\)減るという意味になる。ところが運動量\(mv\)は\(v\)に比例しているから、運動量が減るとは、\(v\)が減る、減速するということに他ならない。Bに追突する側のＡの速度は、Bから左向きに\(F_1\)を受けて確かに減る。
　一方、(2)の力積\(I_2\)は正で、例えば\(I_2=+5\)、力積\(+5\)の分、運動量が\(+5\)変化する、増える、つまり\(v\)が増える、加速するという意味。Aから追突される側のBの速度は、Aから右向きに\(F_2\)を受けて増える。
　さて、作用反作用の法則により、図２で\(|F_1|＝|F_2| \)が成り立ち、ゆえに\(|I_1|＝|I_2| \)も成り立つ。つまり、例えば\(I_1=-5 \)に対して\(I_2=+5 \)。ということはAの運動量の減少分とBの運動量の増加分が(ともに5で)等しい。　　(☆)
　すると、AとBの運動量の合計は、一方でAが減り、他方でBがちょうどそれと等しく増えているのだから、変わらないはずである。そのことを確かめよう。(1)+(2)より
　\((m_1v’_1+m_2v’_2)-(m_1v_1+m_2v_2)=I_1+I_2=0 \)　
　　　（例えば\(I_1+I_2=-5+5=0\) ということ）
　∴　\(m_1v’_1+m_2v’_2=m_1v_1+m_2v_2 \)　　　　　　　　　　　　　　 (3)　
　左辺は２物体A,Bの衝突あとの運動量の合計、右辺は衝突まえの合計。あと=まえ、合計が一定のままであるのを保存するというから、(3)を運動量保存の法則という。

　ここで、運動量保存則が成り立った理由をもう少し詳しく詰めていこう。まず、内力、外力という言葉の定義から。
　\(F_1,F_2 \)はいま注目している２物体A、Bどうしで及ぼし合う作用反作用のペアで、これらを内力という。内力は作用反作用であるがゆえに、(☆)で述べた「一方の運動量の減少と他方の運動量の増加が等しい」条件が成り立つから、運動量の合計は一定のまま、つまり保存する。
　これに対して、図３のように、注目している２物体以外（例えば手）から加わる力を外力という。この場合、Bに加わった外力による力積の分だけBの運動量は増えるが、その分だけAの運動量は減ったりしない（Aに力積は加わっていない）。ゆえに(☆)の条件が成り立たず、運動量の合計は変化する、つまり保存しない。

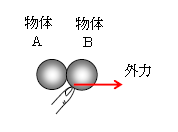
　以上から、内力のみで、外力がなければ運動量は保存することが分かる。
　内力と外力は明らかに反対語だから、「内力のみ」という表現と、「外力がなければ」という表現は、同じことを言っている。しかし、1-32-1２体問題などで、「外力がなければ」の方が「内力のみ」よりも余程使い勝手が良いと実感できるはず。ゆえに当面は、「外力がなければ運動量保存」と覚えるに限る。（ただし、電磁気分野に入ると「内力のみ」の方が役に立つ例もごくわずかある。そのときはまた、この単元に立ち戻ることとしよう）