1-16-3: 2次元の運動エネルギーと仕事（続き）

2次元での運動エネルギーと仕事の関係は、1次元の場合を一般化したもの、それをしっかり押さえましょう。　
→　関連事項はは10-04-1: 力学的エネルギー保存則 の証明へ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　1-16-2最後の式　$\displaystyle \Delta \left( \frac{m}{2}|\vec{v}|^2 \right) =|\vec{F}|\cos\phi \cdot |\Delta \vec{r}|$　ただし$\Delta \vec{r}→ \vec{0}$　　(1)
　（$\phi$は$\vec{F}$と$\Delta \vec{r}$のなす角）　　をこの単元の出発点とする。
　図１のような曲線の軌道を$n$個の線分(黄色)に分割し、それぞれを変位$\Delta \vec{r_1},\Delta \vec{r_2}, \cdots, \Delta \vec{r_n}$と名付ける。最終的には$\Delta \vec{r_k}→\vec{0}$（$k=1,2,\cdots,n$）の極限を取るから、線分ごとの運動と曲線運動は一致する。$k$番目の拡大図が図２。これに(1)を適用すると、
　$\displaystyle \frac{m}{2}|\vec{v_k}|^2- \frac{m}{2}|\overrightarrow{v_{k-1}}|^2 = |\vec{F_k}|\cos\phi_k \cdot |\Delta \vec{r_k}| \;$ 　　　　　　　　　　　　(2)

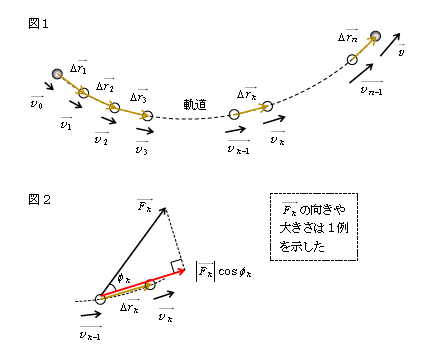
　再び図１に戻って、(2)を$k=1,2,3,\cdots,n$番目について書くと、
　　$\frac{m}{2}|\vec{v_1}|^2- \frac{m}{2}|\vec{v_0}|^2 = |\vec{F_1}|\cos\phi_1 \cdot |\Delta \vec{r_1}|$ 　[ $\vec{F_1},\phi_1$は図示していない ]
　　$\frac{m}{2}|\vec{v_2}|^2- \frac{m}{2}|\vec{v_1}|^2 = |\vec{F_2}|\cos\phi_2 \cdot |\Delta \vec{r_2}|$
　　$\frac{m}{2}|\vec{v_3}|^2- \frac{m}{2}|\vec{v_2}|^2 = |\vec{F_3}|\cos\phi_3 \cdot |\Delta \vec{r_3}|$
　　　　$\cdots \cdots \cdots$
　　$\frac{m}{2}|\vec{v}|^2- \frac{m}{2}|\overrightarrow{v_{n-1}}|^2 = |\vec{F_n}|\cos\phi_n \cdot |\Delta \vec{r_n}|$
　これら$n$個の式を足すと、左辺が数学の「部分分数分解」のようにして$\frac{m}{2}|\vec{v}|^2- \frac{m}{2}|\vec{v_0}|^2$ となり、右辺は和の記号を用いて書けるから、結局次のようになる。
　$\displaystyle \frac{m}{2}|\vec{v}|^2- \frac{m}{2}|\vec{v_0}|^2 =\sum_{k=1}^{n} |\vec{F_k}|\cos\phi_k \cdot |\Delta \vec{r_k}|$　　(＊)　
　物理では、添え字$k$を省き、さらに和の記号も$\displaystyle \sum_{\Delta \vec{r}}$のように書いて、右辺を$\displaystyle \sum_{\Delta \vec{r}}|\vec{F}|\cos\phi \cdot |\Delta \vec{r}|$　のように略記することが多い。　
　ここで$\Delta \vec{r}→\vec{0}$の極限を取っていたことを思い出そう。$\Delta \vec{r}→\vec{0}$での(＊)の右辺を仕事$W$と定義(1-02-1)する。
　$\displaystyle W=\lim_{\Delta \vec{r}→\vec{0}} \sum_{\Delta \vec{r}}|\vec{F}|\cos\phi \cdot |\Delta \vec{r}|$$\;$　　　　　　　　　　　　　　　　　　(3)　
　すると(＊)より、　
　　　　$\displaystyle \frac{m}{2}|\vec{v}|^2- \frac{m}{2}|\vec{v_0}|^2$ $=$　$\displaystyle W=\lim_{\Delta \vec{r}→\vec{0}} \sum_{\Delta \vec{r}} |\vec{F}|\cos\phi \cdot |\Delta \vec{r}|$　　　　(4)
これが　運動エネルギー変化 ＝　仕事　　の式である。
　(3)を見ると、$|\vec{F}|\cos\phi$は図２より力$\vec{F}$のうち物体の移動方向$\Delta \vec{r}$に沿う成分。$|\Delta \vec{r}|$は微小な距離。ゆえに(3)の2次元運動の仕事$W$は「(力の移動方向成分)×(微小距離)を足し上げたもの」というような意味になる。これは、1-16-1の単純な1次元運動の仕事$W$=(力の移動方向成分)×(距離)を一般化したものになっている。
　また、振り返ってみれば(4)を導くのに用いたのは、運動エネルギー$K$と仕事$W$の定義、運動方程式$\displaystyle m\frac{d\vec{v}}{dt}=\vec{F}$、及び数式変形のみである。
　この(4)を押さえれば、10-03-2: 位置エネルギー 　の本格的な説明や、10-04-1: 力学的エネルギー保存則の証明　などへと話が広がっていく。

　さて、1-16-2の通り2次元の運動エネルギー$K$は定義により$\displaystyle K=\frac{m}{2}|\vec{v}|^2$$\displaystyle =\frac{m}{2}({v_x}^2+{v_y}^2)$ だった。ということは、$K$には$v_x$と$v_y$両方を含めなければならない。言い換えると、(4)は$x$成分の式、$y$成分の式のように別々に立ててはいけない。とりわけ左辺は、速さ$|\vec{v}|$(や$|\vec{v_0}|$)丸ごとの2乗をとるのだ。
　運動方程式$m\vec{a}=\vec{F}$のように、$x$成分の式$ma_x=F_x$ と$y$成分の式$ma_y=F_y$を別々に立てられるのを「ベクトル式」という。これに比して、(4)のように別々に立ててはいけないのは「スカラー式」という。もう気付いている人もいるだろうが、(4)の左辺に現われる$\vec{v}$の大きさ$|\vec{v}|$は数学的にはスカラー量である。また、(4)の右辺の$|\vec{F}|\cos\phi \cdot |\Delta \vec{r}|$は内積$\vec{F} \cdot \Delta \vec{r}$と書き換えられ（1-16-2の冒頭の(☆)参照）、内積もまた数学的にはスカラー量である。ゆえに(4)はスカラー式となる。エネルギーも仕事も、ベクトル量ではなくスカラー量である。

<補足>　(4)の右辺の仕事を大学では　$\displaystyle W=\int_C \vec{F} \cdot d\vec{r}$　のように書く。$\displaystyle \int_C$ は「線積分」の記号で、「(曲線)軌道$C$に沿って積分せよ」というほどの意味。