5-04-2: 気体分子運動論 #その2

(I)圧力のまとめは、「気体分子運動論」の最終単元5-04-3でやります。　→　＜#その1＞は5-04-1、＜#その3＞は5-04-3へ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

(I) 圧力　

　図１は前の単元5-04-1の図２の再掲。立方体の面は全部で6枚あるが、どの面についても説明としては同様になるから、右の面だけ注目していくことにする。

　①　1分子が1回の衝突で壁に及ぼす力積 \(=(-1)×\)(分子の受ける力積(赤丸付き矢印))　というように\((-1)\)倍の式変形をしてみる。なぜなら「分子が壁に及ぼす力」の反作用が「壁が分子に及ぼす力」だからで、そうすると力積＝運動量変化の関係を利用して計算が進む。つまり、
　　　　　　　　　　　　　　　　　　　　　　　　 あと　ー　まえ
　　①\(=(-1)×\)(分子の運動量変化)\(=(-1)×(m(-v_x)-mv_x)=\)\(2mv_x \)

　さて、分子の中には速いものも遅いものある。速いものは右の壁に衝突後再び右の壁に戻ってくるまでの時間が短いので、単位時間当たりの衝突回数が多い。遅いものはその逆で衝突回数が少ない。どちらがマクロな圧力に大きく寄与するかと言えば前者。そこで圧力を考えるには以下の②が欠かせないだろう。
　②　1sあたりの衝突回数
　図1で分子運動の\(x\)成分だけを追うと、右の壁に衝突してから再び右の壁に戻ってくるまでに、分子は\(x\)方向に往復\(2L\)進む。ということは図２より
　　②\(=\)\(\displaystyle \frac{v_x}{2L}\)　（図2の例では3回）

　ここで①×②としてみる。①（1分子が1回の衝突で壁に及ぼす力積）× ②（1sあたりの衝突回数）=（1分子が1sあたり壁に及ぼす力積）になることは、日本語的に自明だろう。念のため数値例を挙げると、①（1回の力積）が10[N\(\cdot\)ｓ]で、②（1sあたりの回数）が3[1/s]ならば、①×②=30 [N\(\cdot\)ｓ×1/s=N] は確かに（1sあたりの力積）である。しかも（1sあたりの力積）は単位が[N]の 力 だから、我々のゴールの圧力にぐっと近づく。　(#)
　③　1分子が1sあたり壁に及ぼす力積＝①×②\(\displaystyle =2mv_x × \frac{v_x}{2L} =\)\(\displaystyle \frac{m{v_x}^2}{L} \)
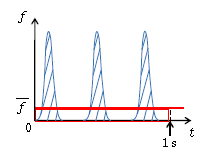
　1-31-1で小球どうしが衝突時に及ぼし合う力\(F\)と時間\(t\)の\(F\)-\(t\)グラフを扱ったが、分子と壁の及ぼし合う力\(f\)の\(f\)-\(t\)グラフも同様になる（図3）。分子が壁に衝突中のごく短い時間だけ\(f\)は大きくなるが、容器を飛来中は\(f=0\)。このように\(f\)の時間変化は複雑だ。ところが③の式は明らかに定数。ということは、
　　③＝1分子が壁に及ぼす力の時間平均（力を時間的に一定とみなしたもの）\(\overline{f} \)
であることが分かる（図３の縦軸に記した）。

　④　③を分子数\(N\)個分合計すれば、分子全体が壁に及ぼす力\(F\)が得られる。ここで、分子に1,2,…,Nのように番号を付け、それらの速さをそれぞれ\(v_1,v_2,\cdots,v_N\)とすれば、分子1番の③は\(\displaystyle \frac{{mv_{1x}}^2}{L} \)、分子2番の③は\(\displaystyle \frac{{mv_{2x}}^2}{L} \)、… のようになるから、それらの合計は
　　④\(\displaystyle =F=\frac{m}{L} ({v_{1x}}^2+ \cdots +{v_{Nx}}^2)\)　＜ \(N\)をかけて\(N\)で割ると同値変形 ＞
　　　\(\displaystyle =\frac{m}{L}N \left[\frac{1}{N} ({v_{1x}}^2+ \cdots +{v_{Nx}}^2) \right] \)　＜ [ 　] は\({v_{〇x}}^2\)を\(N\)個足して\(N\)で割っているから\({v_x}^2\)の(\(N\)個の集団についての)平均値を表し、これを\(\overline{{v_x}^2} \) と書く ＞
　　　\(\displaystyle =\frac{m}{L}N\overline{{v_x}^2} \)　 ＜ ③の時間平均を\(\overline{f}\)と表す一方、④の集団平均は\(\overline{{v_x}^2} \) と書かずに\(<{v_x}^2> \)と書くこともある ＞
　 \(N\)をかけて\(N\)で割った理由は ―― いま\(N\)が10\(^{23}\) 程度の膨大な数の集団を扱っているので、各々の\(v_{1x},v_{2x},\cdots \)はばらばらの値を取り、各々を扱うのは見通しが悪い。大集団を扱うときは平均量に着目するのがよい。
　さて、①(1回の力積)に②(1sあたりの衝突回数)をかけて③(1分子の力の時間平均)を得たのであるが、これを④10\(^{23}\) 程度分合計したものは、
　　④=分子全体が壁に及ぼし続ける力\(F\)　である（図４を見て想像してほしい）。かように、マクロな量は連続量になっている。

　⑤　圧力\(P\)は単位面積当たりの力だから、\(\displaystyle F=\frac{m}{L}N\overline{{v_x}^2} \)を(正方形の)壁の面積\(L^2\)で割って
　　⑤＝\(\displaystyle P=\frac{m}{L^3}N\overline{{v_x}^2}=\frac{Nm\overline{{v_x}^2} }{V}\)　（\(V\)は(立方体の)容器の体積）

　最後に \(\overline{{v_x}^2}= \overline{{v_y}^2}=\overline{{v_z}^2} \)　　(＊)　　
であることに注意しよう。これの成り立つ理由は、10\(^{23}\) 程度の無数の分子が各々ばらばらの速度で動いているのだから、\(x\)方向の平均も\(y,z\)方向の平均も差が付くはずはないという直観的な理由である。[ これ以上は大学の話になるので深入りしない。] すると、　
　⑥　\(\displaystyle \overline{{v_x}^2}= \overline{{v_y}^2}=\overline{{v_z}^2}=\frac{1}{3} \overline{{v}^2} \)　　(☆)　
であることが次のように示せる。
　　右辺の\(\displaystyle \overline{{v}^2}=\frac{1}{N}( \overline{{v_{1}}^2}+\overline{{v_{2}}^2}+ \cdots +\overline{{v_{N}}^2} ) \)　＜ 三平方の定理で\(\overline{{v_{1}}^2}\)、\(\overline{{v_{2}}^2}\)、…、\(\overline{{v_{N}}^2}\)を展開 ＞
　　\(\displaystyle =\frac{1}{N}(\: (\overline{{v_{1x}}^2}+\overline{{v_{1y}}^2} +\overline{{v_{1z}}^2}) + (\overline{{v_{2x}}^2}+\overline{{v_{2y}}^2} +\overline{{v_{2z}}^2}) \)
　　\(\displaystyle +\cdots+ (\overline{{v_{Nx}}^2}+\overline{{v_{Ny}}^2} +\overline{{v_{Nz}}^2})
\: ) \)　＜ まず\(x\)成分をかき集め、次に\(y\)、最後に\(z\)成分 ＞
　　\(\displaystyle =\frac{1}{N}(\overline{{v_{1x}}^2}+\cdots+\overline{{v_{Nx}}^2})+\frac{1}{N}(\overline{{v_{1y}}^2}+\cdots+\overline{{v_{Ny}}^2})+\frac{1}{N}(\overline{{v_{1z}}^2}+\cdots+\overline{{v_{Nz}}^2}) \)
　　\(\displaystyle =\overline{{v_x}^2}+\overline{{v_y}^2}+\overline{{v_z}^2}=3\overline{{v_x}^2} \)　＜ (＊)を用いた ＞　　よって(☆)が言えた。
　(☆)のように書きかえるのは、(＊)が成り立っているからには\(x\)成分だけ特別扱いしたりせず\(\overline{v^2}\)を用いるという意味合いがある。

　⑥を⑤に代入すると　\(\displaystyle P=\frac{Nm\overline{v^2} }{3V}\)　これが分子運動論における(I)圧力公式である。まとめは5-04-3で、(II)(III)とともに扱うことにしよう。