1-11-1: 水圧
水圧を扱うときの水柱の考え方をマスターしましょう!
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント 1-07-1と同様に「力の規則」を示す
| 何から | 向き | 大きさ | |
| 圧力 による力 | 周りの液体 ・ 気体から | 面と垂直 物体を押す向き | 力\(F=PS\) \(P\): 圧力[Pa] \(S\): 面積[m\(^2\)] |
水というと、運動状態の水(流水)もあれば、静止状態の水(静水)もあるが、ここではもっぱら静水を扱う。
水中の物体には、周りの水から押す力が働く。なぜなら、水は無数の分子から成り立っていて、それらが物体に衝突してくる効果が物体を押す力となって表れるからだ(図1)。
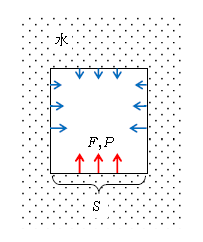
ある面全体に加わる力\(F\)を、その面の面積\(S\)で割って\(\)1m\(^2\)あたりの力に直したものを、圧力\(P\)と呼ぶ・名付ける。1-02-1でやった定義式だ。
圧力\(\displaystyle P=\frac{F}{S} \) (1)
(ただし、\(P\)は面全体にわたって一定とする)。右辺の単位は[N/m\(^2\)]だが、これを省略して[Pa](パスカル)という。すなわち[Pa=N/m\(^2\)]。
圧「力」とは言うが、力[N]ではなく、1m\(^2\)あたりの力[N/m\(^2\)]なので注意。例えば圧力\(P\)が与えられたなら、(1)より
面全体に加わる力\(F=PS\) (\(F=P\)ではない)。
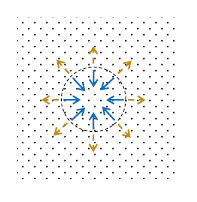
圧力(による力)についても作用反作用の法則が成り立つ。図2で球形の外部にある水が内部を押す圧力(による力)が実線矢印で、球形の内部にある水が外部を押す圧力(による力)が点線矢印。実線矢印と点線矢印は逆向きで大きさが等しい。
辺り一面が水で満たされた(他に何もない)領域を考える。すると、水圧(水の圧力)に関して重要な定理「同じ深さでの水圧は等しい」が導かれる。理由は ―― 図3のように、水の中のある領域を(頭の中で)点線で囲み、水柱と呼んでおく。水柱の形は、ここではきわめて背の低い直方体に選ぶ。水柱自体が静止した水だから、力のつり合いを考えることができる。1-05-1で述べた通り、物体の速度を変化させる原因(力)は必ず他から(周囲から)働くので、水柱に周りから働く力を書き込めばよい。水平方向だけ書くと、左側の水が水柱を押す力\(P_1 S’\)。右側の水が水柱を押す力\(P_2 S’\)。
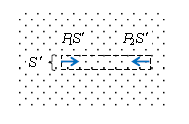
水平方向のつり合い \(0=P_1 S’ -P_2 S’\)
ゆえに\(P_1 =P_2 \)となって、確かに同じ深さでの水圧は等しい。
では、深さ\(h\)での水圧\(P\)を求めよう。今度は、図4のような水柱のつり合いを考える。水柱に周りから働く力を書き込む。力の書き込み方は1-07-1でやったことを思い出そう。
1.地球から重力\(W\)(とおく) ―― この手の問題では、通常、水の密度\(\rho \)[\(\text{kg} \)/m\(^3\)]が与えられる。水柱の体積\(V=Sh\)[m\(^3\)]だから、
水柱の質量\(m=\rho V =\rho Sh \)
[\(\text{kg} =\text{kg} \)/m\(^3\)×m\(^3\)]
ゆえに重力\(W=mg=\rho Shg \) [ 単位を意識しながら計算するのがコツ ]
2.ふれているものから ―― 上側の空気から大気圧\(P_0\)による力\(P_0 S\)。下側の水から水圧\(P\)による力\(P\)。なお、「同じ深さでの水圧は等しい」ので、左右の水から加わる水圧はキャンセルする。
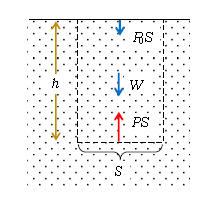
鉛直方向のつり合い \(0=PS-P_0 S-\rho Shg \) よって
水圧\(P=P_0+\rho gh \) (2)
この式より、深さ\(h\)(水面からの距離)が大きいほど\(P\)は大きいから、深い所ほど水圧は大きいと分かる。図4で深くなって\(h\)が大きくなればなるほど、水中の重力\(W\)が増し、それを下支えする水圧の力\(PS\)も大きくなるという意味。
この水圧の公式(2)は単に暗記するのではなく、むしろ水柱のつり合いという考え方自体をマスターしておこう。その方がいろいろな問題に対処しやすい。


