5-04-1: 気体分子運動論 #その1

気体分子運動論のイントロダクションです。　→　＜#その2＞は5-04-2、＜#その3＞は5-04-3へ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　まずはミクロ、マクロという語の説明から。
　原子分子以下のレベルの量を微視的あるいはミクロな(microscopic)量という。分子1個の半径(10\(^{-10}\)m程度)や質量(10\(^{-26}\text{kg}\)程度)がその例。気体分子の速さは500m/s(!)程度と大きいが、分子1個の量だからミクロに分類される。
　我々が感知できる程度に大きかったり、アボガドロ定数程度(10\(^{23}\))の大集団のレベルの量を巨視的あるいはマクロな(macroscopic)量という。例えば圧力や体積はマクロな量で、机はマクロな物体。
　タイトルの「気体分子運動論」（略して分子運動論）とは、気体に関するマクロな量（温度など）をミクロに説明する理論である。例えば圧力というマクロな量を、無数の気体分子が容器の内壁を叩き続ける結果というミクロな観点で説明する。
　\(\displaystyle \)当参考書の熱力学分野では、気体と言えば理想気体のことを指すものとする。理想気体とは、気体が十分希薄なときにとるであろう理想形としての気体である。マクロには状態方程式\(PV=nRT\)を満たし、ミクロには分子の衝突時以外は分子間力が無視できる。　　(＊)
　実在の気体は、低温・高圧すぎなければ（常温・常圧では）理想気体と見なせることが実験的に分かっている。

　図1は一辺\(L\)の立方体容器中を飛び回るモル数\(n\)の同種の気体分子（質量\(m\)）の様子。1つの分子の速度ベクトル\(\vec{v}\)及びその成分\(v_x,v_y,v_z\)が示してある。
　力学で2体問題というと問題の難易度が上がる。気体は10\(^{23}\)体問題で、これをまともに扱うことは絶望的。そこで、物事を簡単化する2つの仮定をおく。
　(i)　等速直線運動の仮定: 分子は重力を受けて放物軌道を描くはずであるが、その影響を考えるのは当面後回しにする。(＊)で「分子の衝突時以外は分子間力が無視できる」と述べたが、衝突としては分子と容器の内壁（以後単に「壁」と呼ぶ）の衝突のみを考え、高校物理としては分子どうしの衝突は考えない。
　(ii)　弾性衝突の仮定: 非弾性衝突の効果を取り入れるのは当面後回しにする。

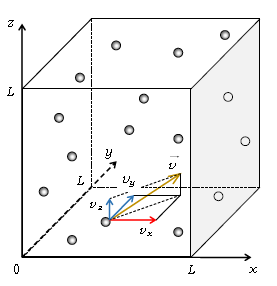
　図２は図１の1個の分子を手前から見た断面図。さて、1-31-2の通り弾性衝突では運動エネルギーが保存するから、衝突前後で\(\frac{m}{2}v^2\)は不変、つまり\(v\)(図２黄色)は不変。運動エネルギーが保存するということは摩擦熱が発生して運動エネルギーが失われることはない。すなわち壁に平行に摩擦力は働かない。「力が加わらないと物体は等速」（ニュートンの運動の第1法則）だから、壁に平行な速度成分\(v_y,v_z\)(青)も不変。また1-30-1の最後の段落にある通り、弾性衝突ははね返り係数が１で、壁(固定面)と分子が斜めに衝突するような場合は固定面に垂直な速度成分の大きさが不変だから\(|v_x|\)(赤)も不変。すると黄、青、赤の成す2つの直角三角形が合同になるから、入射角\(\theta\)＝反射角となる。これを称して「固定面との弾性衝突では等角反射が起こる」という。

　高校物理の分子運動論は3部構成で捉えるのがよい。次の単元5-04-2から(I)マクロな圧力をミクロに説明　(II)マクロな温度をミクロに説明　(III)マクロな内部エネルギーなる量をミクロな観点で導入　の順序で解説していく。なお、分子運動論で用いる「道具」は力学だけで、波動や電磁気などは一切登場しない。