3-14-1: コンデンサーのつなぎ変え ＜例題＞

コンデンサー分野の頻出問題をマスターしましょう！　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　[ この単元ではジュール熱などエネルギーの考察はしていない。]

例題　

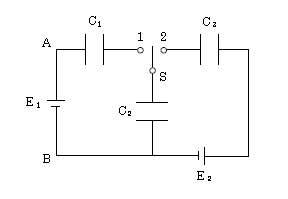
　図の回路でコンデンサーC_１, C_２, C_３の電気容量はそれぞれ\(2C\)、\(C\)、\(2C\)、電池E_１, E_２の起電力はそれぞれ\(2V\)、\(V\)である。 最初各コンデンサーは帯電していなかったとして、以下の問いに答えよ。
(1)  まず、スイッチSを１側に入れた。十分時間がたった後でコンデンサーC_２の下側の極板に蓄えられる電荷を求めよ。
(2)　次に、スイッチSを２側に入れた。十分時間がたった後でコンデンサーC_３の左側の極板に蓄えられる電荷を求めよ。
\(\displaystyle \)(3)　今度は電池E_１を取り外してAB間を短絡し、それからスイッチSを１側に入れた。十分時間がたった後でコンデンサーC_２の下側の極板に蓄えられる電荷を求めよ。  

解答・解説

(1)　左半分の回路（一周する通り道）を考える（図１）。電池E_１の正極から＋の電荷が流れ出すから（自由電子ーの流れと逆向きに＋が流れると言ってもよい。3-01-1)、C_１の左極板の電荷を\(Q\)、C_２の上極板の\(Q’\)とおく。
　図１の赤色を施した部分は、周りとつながっていない。言うなれば宙に浮いたかのような部分で、「電気的に孤立した部分」という。孤立部分はその外から電荷が入ってきたり、外へ電荷が出ていったりしない。このとき孤立部分の電気量の合計は一定のままである。イメージ的には、陸の孤島の人口は人の出入りがないと一定のまま、といった感じ。これを孤立部分の電荷は保存するという。問題文中に「最初各コンデンサーは帯電していなかった」とあるので、赤い部分の電気量は0のまま一定。ゆえに

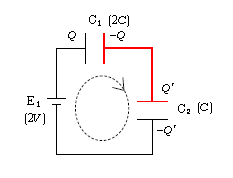
　　孤立部分の電荷保存則：\(-Q+Q’=0\)　　①
　次に、電位差の関係式として、3-13-1のキルヒホッフの第２法則、略してキルヒホッフ則(で通じる)を立てる。3-08-1の公式\(Q=CV\)より電位差\(\displaystyle V=\frac{Q}{C}\)だから、
　　電圧降下　= 起電力（右回りを回路の正の向きとする(図１の点線)）
　\(\displaystyle \frac{Q}{2C}+\frac{Q’}{C}=\) \(2V\)　　　　　　　　　　　　 ②
①、②の連立から\(Q,Q’\)が求まる。
　コンデンサー回路の問題では、コンデンサー中の電場の様子まで調べなくてよいものが多い。このようなときは、3-08-1でやったような第１公式：電荷から電場、第２公式：電場に沿って電位差　の手順は飛ばして、いきなり第３公式：\(Q=CV\)を用いるのが簡単だ。
　①より \(Q’=Q\)　　②に代入　\(\displaystyle \frac{3}{2} \frac{Q}{C} =2V \)　
　∴　\(\displaystyle Q=Q’=\frac{4}{3} CV \)　　　　　　　　　　③
　求めるのはC_２の下極板の\(-Q’=\)　答　\(\displaystyle – \frac{4}{3} CV \)　
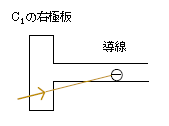
(2)　まず、スイッチSの1側をOFFにすると、図1のC_１右極板の電荷\(-Q\)は動けない。というのも、仮に\(-Q\)の一部が流れ出したとすると、Sの1側がOFFなので電流にとって「行き止まり」の状況。ゆえにC_１の右の導線に⊝または⊕が分布することになるが（図2）、この⊝または⊕のつくる電気力線（黄色）は極板を貫き、3-06-1で述べた導体内部の電場が０であることと矛盾してしまう。このようにしてC_１の右極板の\(-Q\)が動かないということは、3-08-1でやった通りコンデンサーの電荷の組合せは必ず\(+Q,-Q\)であるから、C_１の左極板の\(+Q\)も動けない。（特別な状況でない限り ―― その状況についてはここでは深入りしないが ―― ）電荷が動ける所としては回路（１周の通り道）のみを考えればよい（いまは右半分の回路）。

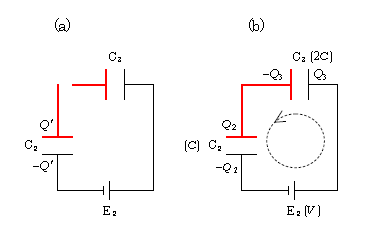
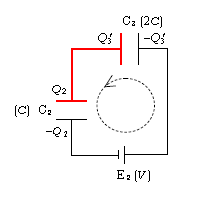
　すると、スイッチSを2側に入れる前の右半分の様子が図3(a)、2に入れた後が図3(b)。電池E_２の正極から電荷が流れ出すだろうから、C_３の右極板の電荷を\(Q_3\)、C_２の上極板の\(Q_2\)とおく。孤立部分に注目する（赤色）。孤立部分は典型的に「極板、導線、極板」のワンセットだ。
　電荷保存：　あと　＝　まえ
　　　　　\(Q_2-Q_3=\) 　\(Q’\)　\(\displaystyle =\frac{4}{3} CV \)　[ ③を代入した ]　　④
　電位差の関係（あとの状態）：電圧降下　＝起電力（左回りが回路の正の向き）
　　　　　　　　　　　　　　\(\displaystyle \frac{Q_3}{2C}+\frac{Q_2}{C}=\)\(V\)　　　　　　　　⑤
　④より \(\displaystyle Q_2=Q_3+\frac{4}{3} CV \)　　　　　　　　　　　　　　　　⑥
　⑤に代入　\(\displaystyle \frac{3}{2} \frac{Q_3}{C} +\frac{4}{3} V =V \)　　∴　\(\displaystyle Q_3=-\frac{2}{9} CV \)　　　⑦
　求めるのはC_３の左極板の\(-Q_3=\)　答　\(\displaystyle \frac{2}{9} CV \)　
　なお、⑥より \(\displaystyle Q_2=\frac{10}{9} CV \)　　　　　　　　　　　　　 　　⑧

　ここで3つ補足しておこう。第1に、図3(b)のように電荷を未知量として置いたが、図4のようにC_３の左極板をプラスで置いてもよい。すると、電荷保存は④の代わりに　
　　\(\displaystyle Q_2+Q’_3=\frac{4}{3} CV \)　　④’　　
　また、左回りを回路の正の向き(電位をたどる向き)とすると、C_３の右\(-Q’_3\)から左\(Q’_3\)へ電位が上がると置いていることになる。3-13-1の通り電位の上がり分は負の電圧降下として扱うから、電位差の関係は⑤の代わりに
　　\(\displaystyle -\frac{Q’_3}{2C}+\frac{Q_2}{C}=\)\(V \, \)　　 ⑤’
　④、⑤の\(Q_3\)を\(-Q’_3\)に書き換えると④’、⑤’に一致している。ということは、\(Q_3\)の値と\(-Q’_3\)の値が一致する、つまりC_３の右極板は\(-Q’_3=Q_3=-\frac{2}{9} CV \) [ ⑦より ] である。
　以上をまとめると ―― 電荷を置くときはどちらを正極板に仮定してもよいが、正極板と仮定した方を高電位側と見なして電位差の関係式を立てること。

　補足の第2：\(Q_3=-\frac{2}{9} CV \)と負の値で求まったということは、C_３の右極板から正電荷が流れ出して、結果\(Q_3=-\frac{2}{9} CV \)の負電荷が残ったということ。すると、電池の正極側から負極側へ電荷\(\frac{2}{9} CV \)が通過したことになる。これを「電池を電荷が逆流した」という。
　補足の第3：3-10-1でやった通り、直列合成容量の公式は直列どうしの２つのコンデンサーの電荷が共通でなければ使えない。ということは、(1)では公式を使えたにせよ(2)では使えない。使える場合も含めて、ポイントにある通り、電荷保存と電位差の関係という統一的なアプローチで攻める方が明快だ。
(3)　まずは(2)終了時点での状態を図5(a)に示す（C_３、E_２は省略した）。C_１に\(Q,-Q\)が残っていたことに注意しよう。問題文中の「AB間を短絡」とは、ABを直接導線でつなぎ、電気抵抗などを一切差し挟まないこと。(3)の操作後の状態を図5(b)に示す。ここで(b)を(c)のように少し書きかえれば、コンデンサーC_１, C_２が並列になっていることが分かる。操作まえの(a)と操作あとの(c)を比べる。孤立部分に注目する（赤色）。

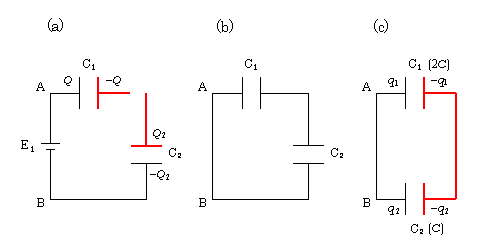
　電荷保存：　あと　＝　まえ
　　　　　\(-q_1-q_2=\)\(-Q+Q_2\)　\(\displaystyle =-\frac{4}{3} CV +\frac{10}{9} CV =-\frac{2}{9} CV \)　
　　∴　\(\displaystyle q_1+q_2=\frac{2}{9} CV \)　　⑨
　電位差の関係（あとの状態）：3-10-1の通り、並列接続では電圧共通だから \(\displaystyle \frac{q_1}{2C}=\frac{q_2}{C} \)
　　∴　\(q_1:q_2=2:1 \)　　　⑩
　⑨で\(q_1\)と\(q_2\)の和、⑩で\(q_1\)と\(q_2\)の比が分かったのだから、
　　\(\displaystyle q_2=\frac{1}{2+1} \frac{2}{9} CV = \)　　答　\(\displaystyle \frac{2}{27} CV \)
　⑩のように、並列の場合は電荷の比が分かるから、計算がしばしば容易になる。